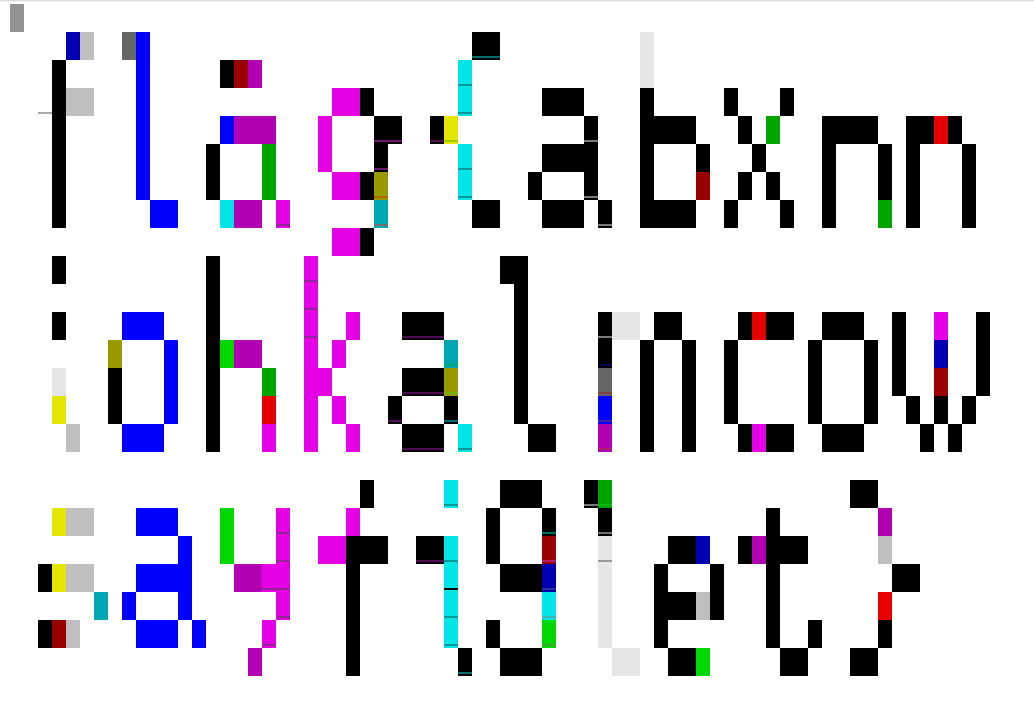这是我个人的 write-up，仅包含我赛时会做的题（其它题看官方题解就好了，没必要再写一遍），记录自己做题时的奇奇怪怪的乱搞方法，仅供参考。

由于我只是个菜鸡，所以解题方法可能会有点绕，可能原理甚至有问题，请大佬原谅我这个菜鸡。

前言

谨以此文纪念我参加的第一场 Hackergame。

Ranking

这次 Hackergame 感觉有比较多的乱搞题（然后才能让我这种乱搞选手能拿到可观的分数）。然后像是比较正经的 binary 题，我是差不多一个都不会做的（比赛结束前 1 天的时候，binary 还是 150）。

目录

没有链接样式的都是不会做的，或者是（对于有多个子问题的题目）没有完全做出来的。

签到

点按钮可以切换 Page，然后不同的 Page 对应不同时间。
并且可以观察到，Page 的 number 就是 Unix 时间戳。
我们不妨大胆猜想，把 Unix 时间戳设置成当前时间，即访问 http://202.38.93.111:10000/?page=1634968833，然后发现就可以获得 Flag。

进制十六——参上

观察到右边的 flag 被遮住了，但是左边的 hex 却没有被遮住。所以就可以解析左边的 hex 得到右边的 flag：

1
2
3
codecs.decode(
    '666c61677b5930555f5348305531445f6b6e30775f4830575f74305f43306e763372745f4845585f746f5f546578547d',
    'hex')

去吧！追寻自由的电波

下载音频，发现音频播放速度非常快，大概是被暴力压缩了。
我们可以随便找点软件（我用了手边的 iMovie），把音频放慢，就可以听了。

题目云「使用了无线电中惯用的方法来区分字符串中读音相近的字母」，即 e 用 echo 表示，等。 虽然英语听力不太行，但是听首字母还是能勉强听得出来的。

小彩蛋(?)：把音频放的没那么慢，可以听到女声；再放慢点，就变成了男声，这就说明……（逃）

猫咪问答 Pro Max

  1. 2017 年，中科大信息安全俱乐部（SEC@USTC）并入中科大 Linux 用户协会（USTCLUG）。目前，信息安全俱乐部的域名（sec.ustc.edu.cn）已经无法访问，但你能找到信息安全俱乐部的社团章程在哪一天的会员代表大会上通过的吗？
    提示：输入格式为 YYYYMMDD，如 20211023。请不要回答 “能” 或者 “不能”。

看到「已经无法访问」，直接下意识想到 web.archive.org。

在 web archive 里打开 sec.ustc.edu.cn，找到章程，然后就找到其通过日期为 2015 年 5 月 4 日。

  1. 中国科学技术大学 Linux 用户协会在近五年多少次被评为校五星级社团？
    提示：是一个非负整数。

查资料无果（可能我姿势不对），先下一题。

  1. 中国科学技术大学 Linux 用户协会位于西区图书馆的活动室门口的牌子上“LUG @ USTC”下方的小字是？
    提示：正确答案的长度为 27，注意大小写。

经过多次搜索尝试，在 Google 搜索 “LUG USTC” 并切换至“图片”一栏，就可以发现这么一张照片：

即 “Development Team of Library”，刚好是 27 个字。

  1. 在 SIGBOVIK 2021 的一篇关于二进制 Newcomb-Benford 定律的论文中，作者一共展示了多少个数据集对其理论结果进行验证？
    提示：是一个非负整数。

搜索 “SIGBOVIK Newcomb-Benford”，然后就能找到一篇论文（集）：SIGBOVIK 2021。

通过目录找到这篇文章，然后仔细阅读，并且与作者友善探讨学术问题（大雾）。

实际上通过简单提取，不难发现附录的 figures 都是数据集，一共有 14 - 1 = 13 个

  1. 不严格遵循协议规范的操作着实令人生厌，好在 IETF 于 2021 年成立了 Protocol Police 以监督并惩戒所有违背 RFC 文档的行为个体。假如你发现了某位同学可能违反了协议规范，根据 Protocol Police 相关文档中规定的举报方法，你应该将你的举报信发往何处？
    正确答案的长度为 9。

搜索 “IETF Protocol Police”，不难找到 RFC 8962。

直接搜索关键词 (e)mail 或 send，不难找到「Send all your reports of possible violations and all tips about wrongdoing to /dev/null.」（不得不说，这个玩笑开得真是可以）。

所以答案就是 /dev/null，长度也刚好是 9。

（手动分割线）

然后至此我们找到了 1, 3, 4, 5 的答案，还剩下的第 2 题，可能的答案只有 6 种，手动枚举一下即可（居然是 5 次，我还以为是 0）。

卖瓜

说实话，我猜不出它（服务器 PHP 代码）是怎么算的，然后就搞不清楚具体是怎么溢出的，但是还是可以瞎试。

完了，我忘记我当时是怎么试的了。

Update：我想起来了。

首先，盲猜一下数值的范围是 2632^{63}263 以内，然后整 ⌊2639⌋+1 + 1⌊9263​⌋+1（1024819115206086201）个 9 斤的瓜，这样乘一下恰好能超过范围。

提交一下，得到「电子秤上已有 -9223372036854775808/20 斤的瓜」。

再加上 1024819115206086200（比上面少 1）个瓜，就变成了「电子秤上已有 -8/20 斤的瓜」。

接下来再买 1 个 9 斤瓜，再买 1024819115206086201 个，再买 1024819115206086200 个，此时，就有：「电子秤上已有 -7/20 斤的瓜」。

此时再买上 3 个 9 斤瓜，就可以刚好到 20 斤，就「恭喜你逃过一劫！」。

上面的操作不能合并，不要问我为什么，我也不知道。我只是瞎试的。

透明的文件

打开文件，发现里面的字符好像 \033 控制符（然后就是缺了 \033）。不妨试试在 [ 前都加上 \033（据说 \033 后面一定会接着 [）。

然后打印之，可得：

不难读出，flag 是 flag{abxnniohkalmcowsayfiglet}。

附读取程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <cstdio>

char buffer[20 * 1024];

int main() {
    FILE *f = fopen("transparent.txt", "rb");

    fseek(f, 0, SEEK_END);
    int size = ftell(f);
    rewind(f);

    fread(buffer, 1, size, f);
    for (int i = 0; i < size; i++) {
        if (buffer[i] == '[')
            putchar('\033');
        putchar(buffer[i]);
    }

    return 0;
}

旅行照片

读题，发现题目的着重点在 KFC 上，并且其非常近海，猜想符合条件的 KFC 不多。
于是搜索 “海边 KFC”，虽然不能直接找到目标（大概?），但是过半的搜索结果都是关于“秦皇岛”的。
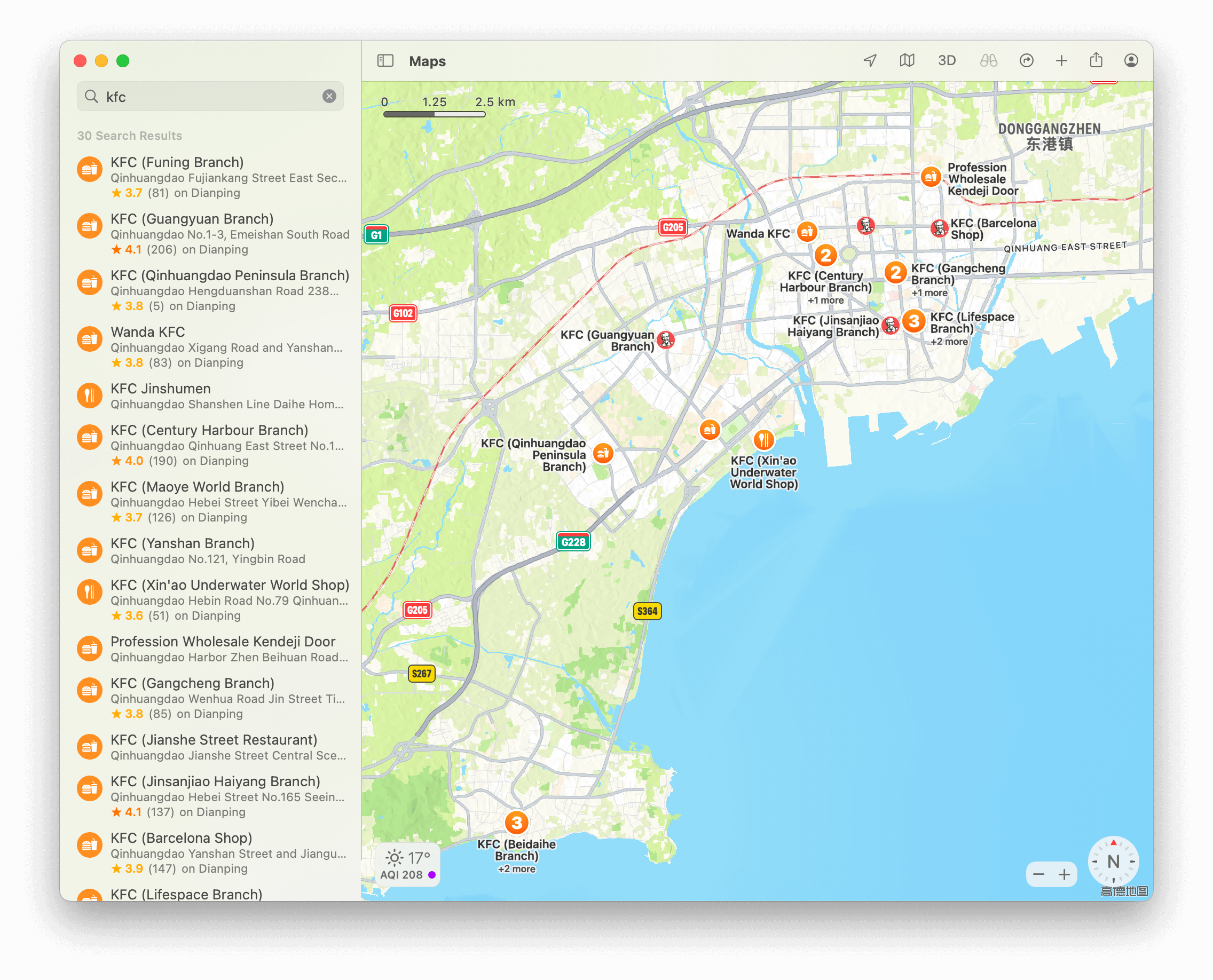
然后打开地图，定位到秦皇岛，查找附近的 KFC，得：

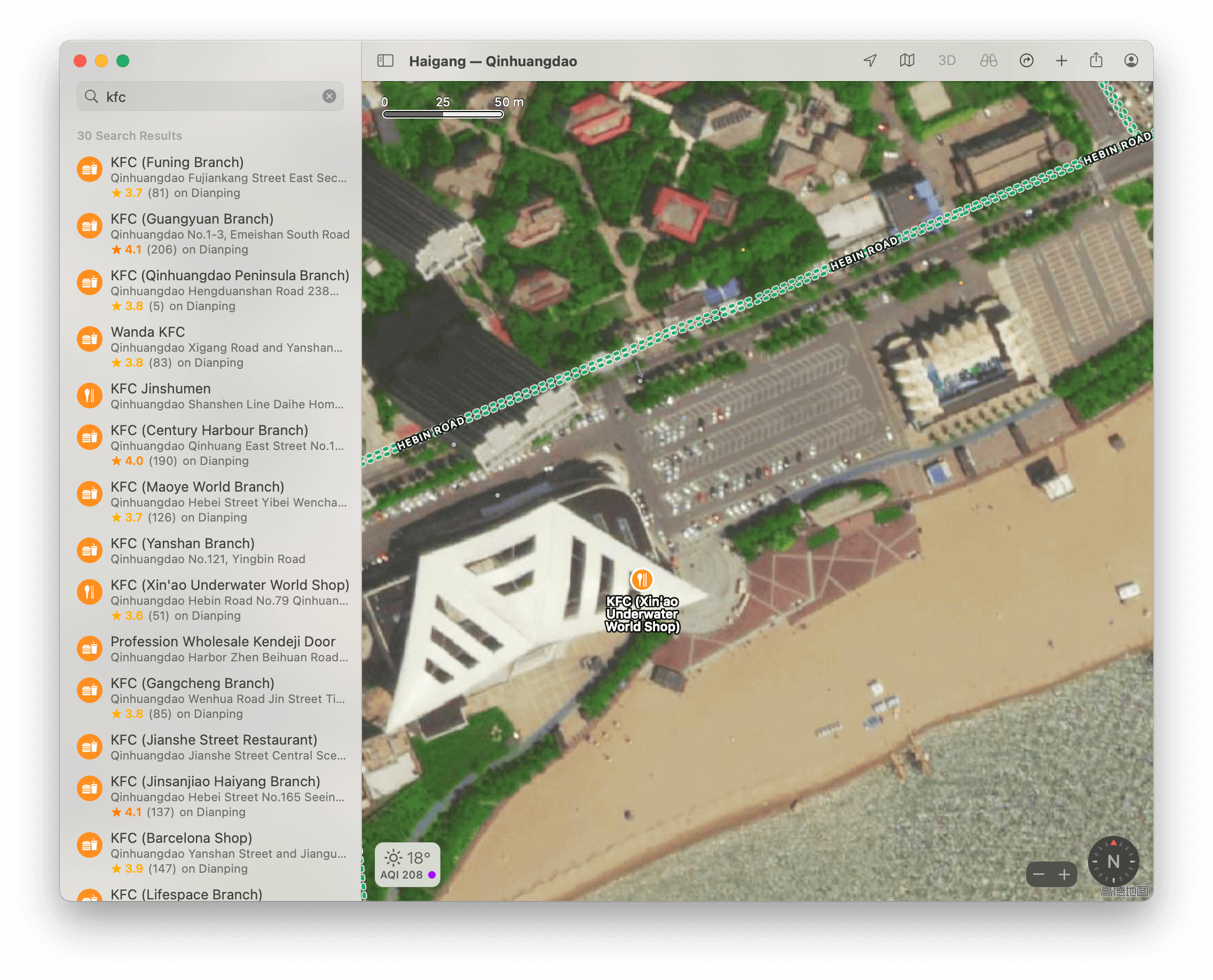
发现有一家 KFC 很接近海，打开卫星图模式，并放大观察：

可以发现停车位对上了，那块覆盖着植被的石头也对上了，虽然 KFC 位置出现了一点偏差，但是不影响做题。

观察原图的停车位方向和阴影方向，不难发现拍摄者面朝东南，时间是傍晚。

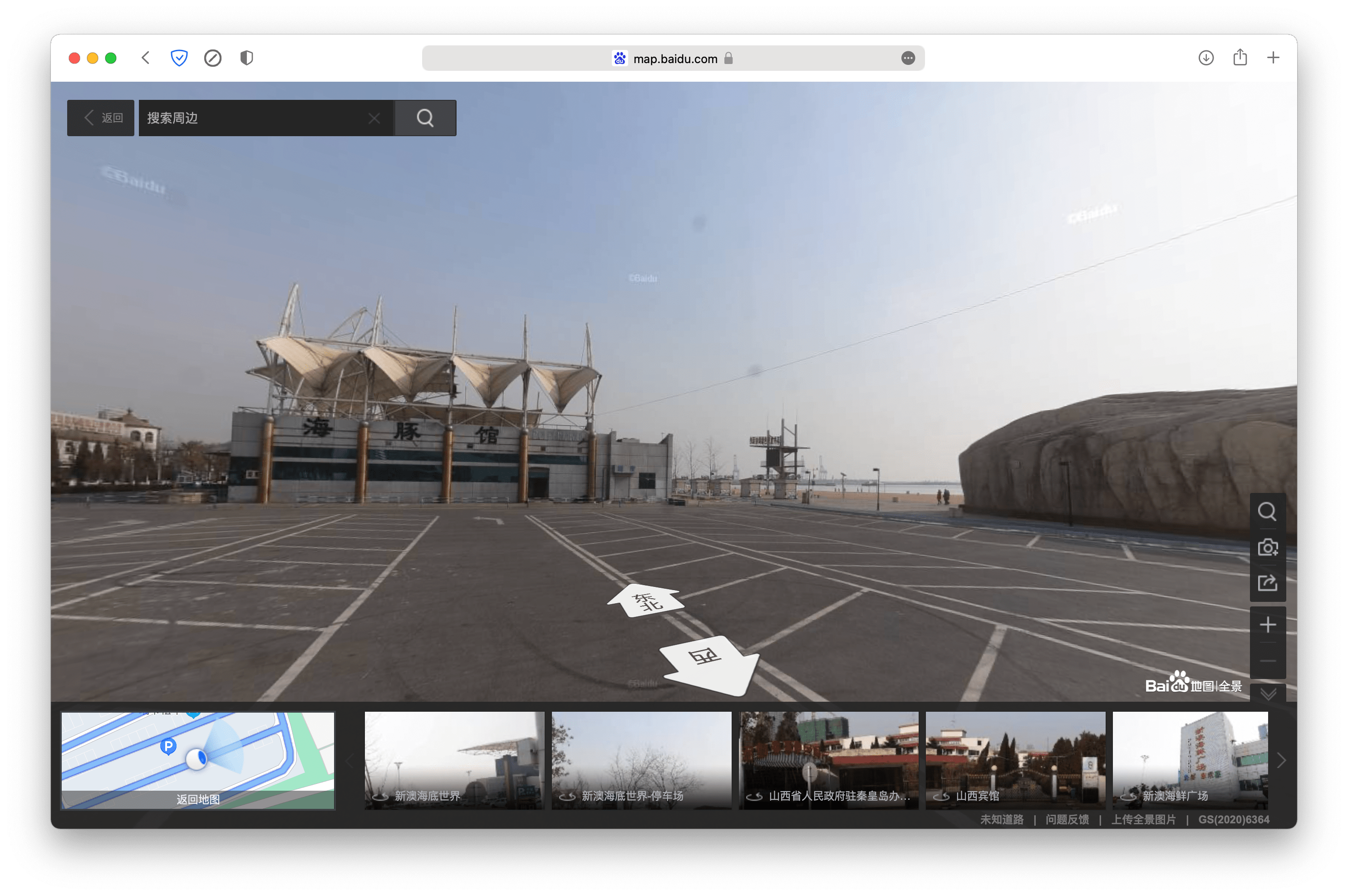
然后打开百度街景（不是广告），观察实地景象。百度街景这都多久没更新了？

虽然没有 KFC，但观察屋顶，还是能确定就是那里的。然后就能确定那三个大字就是「海豚馆」。

然后打开 KFC 门店信息查询，定位秦皇岛。
虽然「新澳海底世界甜品餐厅」没有电话，猜测电话跟旁边的「新澳海底世界餐厅餐厅」一样（0335-7168800）。

最后还剩下楼层高度，看隔壁楼层数一下，大概是在 14 层左右（如果不对就上下多试几层就对了）。

FLAG 助力大红包

总结题意：你需要用 256 个不同的 /8 IP 地址砍红包（访问对应 URL）。

但是这怎么可能呢，有些 IP 段本来就是有保留用途的，而且时间还限制 10 分钟。

经过一番胡思乱想，发现可以通过携带 X-Forwarded-For header 来欺骗，就能轻松砍到 flag。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import requests
import time

for i in range(256):
    while True:
        r = requests.post(
            'http://202.38.93.111:10888/invite/...',
            data={ 'ip': f'{i}.1.1.1' },
            headers={ 'X-Forwarded-For': f'{i}.1.1.1' })

        if '助力成功！' in r.text:
            print(f'Success {i}')
            break
        elif '操作速度太快了' in r.text:
            print(f'Too fast, sleep')
            time.sleep(1)

Amnesia - 轻度失忆

.data 段没了，字符串常量是储存在这里的。既然不能用字符串常量，就分割成字符就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <stdio.h>

int main() {
    putchar('H');
    putchar('e');
    putchar('l');
    putchar('l');
    putchar('o');
    putchar(',');
    putchar(' ');
    putchar('w');
    putchar('o');
    putchar('r');
    putchar('l');
    putchar('d');
    putchar('!');

    return 0;
}

图之上的信息

经过简单尝试（瞎改原请求的参数，然后看错误信息），可以知道 GraphQL 里面有 GUser 类型，其中有 id, username 两个字段。

查 GraphQL 文档，找到“内省”部分，可以用如下代码获取 GUser 的所有字段：

1
{ "query": "{ __type(name: \"GUser\") { name, fields { name }}}"}

得到其所有字段：id, username, privateEmail。

再查询 id 为 1 的 admin 用户的 privateEmail 即可：

1
{ "query": "{ user(id: 1) { id, username, privateEmail }}" }

Easy RSA

观察代码，我们有三个任务：

  1. 计算 p
  2. 通过 value[-1] 反推全部 value
  3. 通过 value_q 反推 q

1. 计算 p

查找资料，可以找到一个叫“威尔逊定理”的东西，即当 p 为质数的时候，有：

(p−2)!≡1(mod⁡p)(p - 2)! 1 ( p)(p−2)!≡1(modp)

则：

y!≡(x−2)!×y!(x−2)!≡1∏i=y+1x−2i≡∏i=y+1x−2inv(i)(mod⁡x)y! (x - 2)! _{i = y + 1}^{x - 2} inv(i) ( x)y!≡(x−2)!×(x−2)!y!​≡∏i=y+1x−2​i1​≡i=y+1∏x−2​inv(i)(modx)

代码：

1
2
3
4
5
def get_p(x, y):
    mul = 1
    for i in range(y + 1, x - 2 + 1):
        mul = mul * pow(i, x, x - 2) % x
    return mul

2. 反推 value

这个部分涉及到一个最主要的函数就是 sympy.nextprime，先看看它的文档：

def nextprime(n, ith = 1)
Return the ith prime greater than n.
See Also: prevprime: Return the largest prime smaller than n.

……我感觉官方文档都告诉你应该怎么做了。

1
2
3
4
5
def get_first_value(last_value):
    val = last_value
    for _ in range(9):
        val = sympy.prevprime(val)
    return val

3. 反推原始 q

这个部分就是给出这个式子（我们把这个原始的 q 称为 x）：

q≡xe(mod⁡n)q x^e ( n)q≡xe(modn)

已知 e, n, q，求 x。

然而我不会求，查资料，发现了这个：Finding the k-th root modulo m，简直完美。

按照这篇文章（回答）所说，首先求满足这一式子的 uuu, vvv：

u e−v φ(n)=1u , e - v , (n) = 1ue−vφ(n)=1

显然 gcd⁡(e, φ(n))=1(e, , (n)) = 1gcd(e,φ(n))=1，这一步可以用 exgcd 做。

求出来了之后，就有

x≡(bu)e(mod⁡n)x (bu)e ( n)x≡(bu)e(modn)

写成代码，就是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 这里的 n 我们通过 `first_value` 生成
def get_original_q(e, q, first_value):
    value = [ first_value ]
    n = first_value
    for i in range(1, 10):
        value.append(sympy.nextprime(value[i - 1]))
        n *= value[-1]

    # 这样求 phi 可以快不少，该函数要求 factors 中的 keys 都是质数。
    factors = { v: 1 for v in value }
    pn = sympy.ntheory.factor_.totient._from_factors(factors)

    # Ex-GCD, 其中 h = gcd(e, pn)；u, v 含义如上所述。
    (u, v, h) = sympy.polys.polytools.gcdex(e, pn)

    x = pow(q, int(u) * e, n)
    return x

经过验证，以上三个脚本算出的结果，代入进源程序中，都可以算出源码中对应的结果。

4. RSA 解密

RSA 解密还需要一个数 ddd（含义请自行翻看 RSA 文档，也可以看这篇）。

这个 ddd 需要满足以下式子：

ed≡1(mod⁡n)ed 1 ( n)ed≡1(modn)

在先进的 Python 3.8+ 中，可以直接用 pow(x, -1, mod) 来算逆元，省事不少。

于是解密部分的代码：

1
2
3
4
5
6
7
8
pn = sympy.ntheory.factor_.totient._from_factors({ p: 1, q: 1 })  # phi(n)

d = pow(e, -1, pn)

c = 110644875422336073...
m = pow(c, d, p * q)
print(m)
print(m.to_bytes(32, 'big'))

然后就可以拿到 flag 了。

加密的 U 盘

通过查询 LUKS 的使用文档，可以发现其可以使用密码或 keyfile 加密，于是大胆猜测改密码不会改变 keyfile 一类的东西（注：实际上是 master key 不会变）。

首先使用 losetup -P /dev/loop1 day1.img 将镜像挂载至 loopback（day2 同理）。

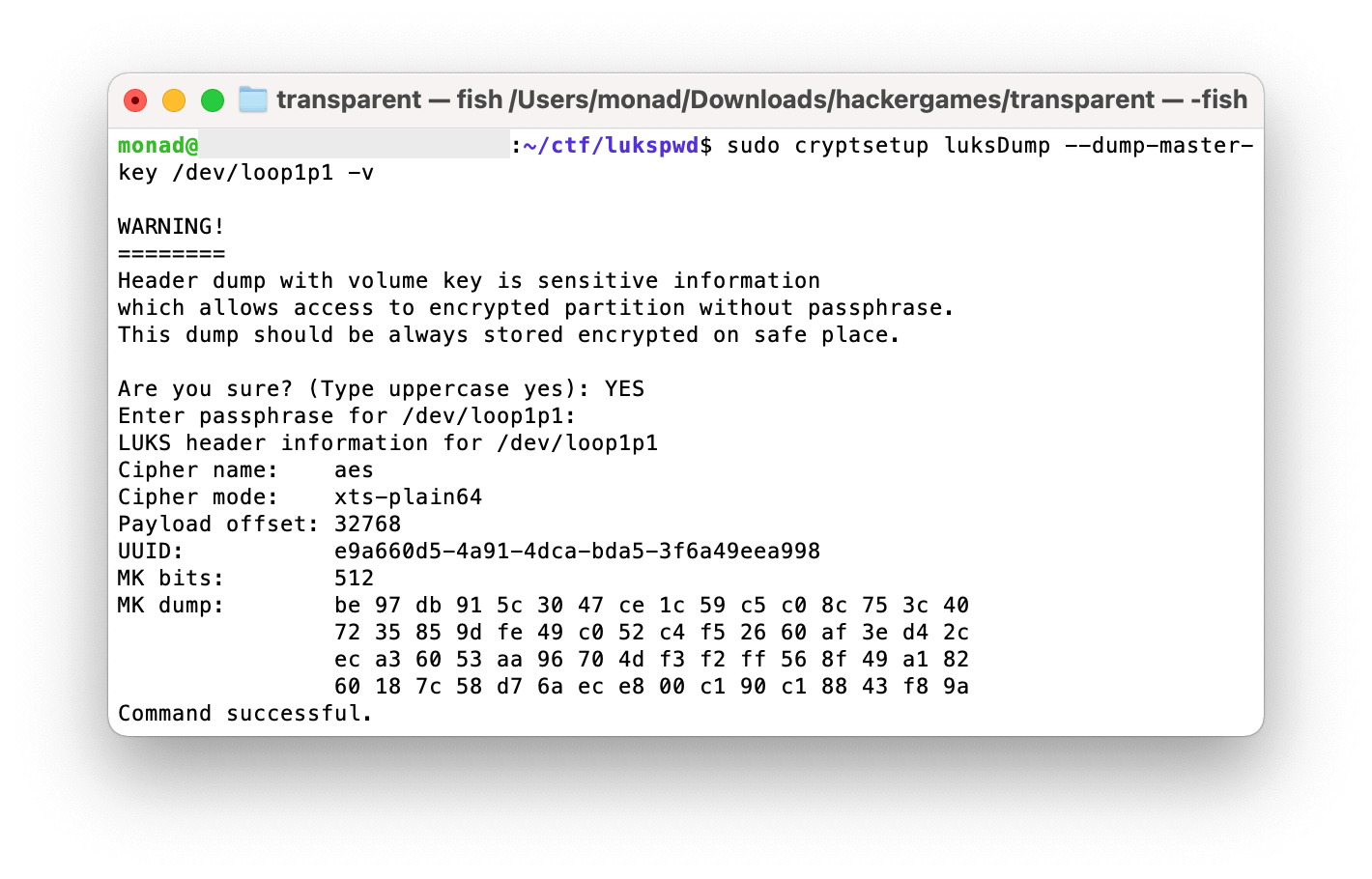
然后用 cryptsetup luksDump --dump-master-key /dev/loop1p1 dump 出 master key。MK dump 里就是 master key。并用 xxd 或其它工具将 master key 写入文件。

接着用 master key 打开 day2.img 即可：sudo cryptsetup luksOpen --master-key-file <key file> /dev/loop2p1 day2。

最后把 /dev/mapper/day2 mount 一下就能读出 flag.txt 了。

赛博厨房

Level 0

写 4 个程序，针对不同菜谱执行不同程序即可。

1
2
3
4
5
6
7
8
9
10
11
向右 x 步
拿起 1 个物品
向下 1 步
向左 x 步
放下 1 个物品
向上 1 步
向右 y 步
拿起 1 个物品
向下 1 步
向左 y 步
放下 1 个物品

自行修改 x, y = 1 or 2 来控制不同菜谱即可。

Level 1

写个简单循环，把物品不断放到锅中即可。

1
2
3
4
5
6
向右 1 步
拿起 100 个物品
向下 1 步
向左 1 步
放下 1 个物品
如果手上的物品大于等于 1 向上跳转 1 行

Level 2

写 32 个程序，第 i 个程序分对应 [0, 0, 0, 0, 0, i] 这个菜谱。 然后再额外加一个程序，写 向右 {} 步，然后枚举数字，撞 hash（实际上是两个 sha256 和一个 arc4 随机?）。

暴力代码见：GitHub Gist 4febc8f。

灯，等灯等灯

Level 0

解一个线性方程组即可。代码过丑就不放了（逃）。

我发现我不会写 % 256 意义下的高斯消元，于是我就直接用 Python 高精度，解完再取模。

然后我解完之后，没有去研究提交的 HTTP API，直接就写了个程序模拟鼠标点击（逃）

Micro World

随便乱瞅一下（我不会告诉你我走了多少弯路的），能发现这个程序是用 pyinstaller 生成的。

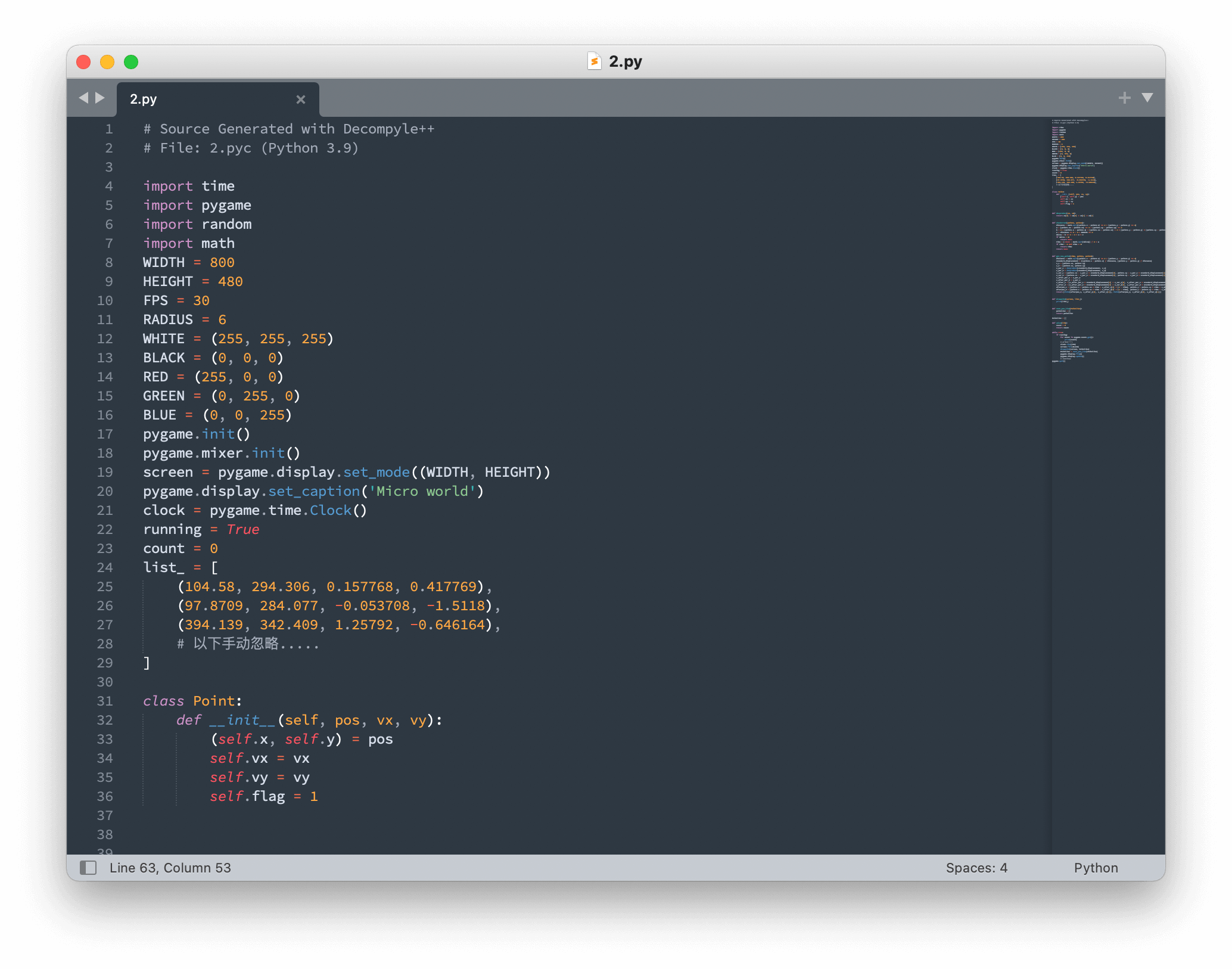
然后就找一个 pyinstaller unpacker（我用的是 extremecoders-re/pyinstxtractor），然后就可以发现一个 2.pyc 文件。用 pip 安装 pygame 后，发现可以直接用 python 2.pyc 运行，能确定提取出了正确的东西。

接着继续尝试反编译，我这里找了 zrax/pycdc，能够逆向 Python 3.9 的字节码，但不完全能逆向出来（但是至少能看到大致的逻辑，也能看到点的数据）。

这是 2.pyc 中 Point 的定义：

1
2
3
4
5
class Point:
    def __init__(self, pos, vx, vy):
        (self.x, self.y) = pos
        self.vx = vx
        self.vy = vy

不难猜出，vx 和 vy 就是这个点的移动速度（也就是 list_ 每个元素的后两个值）。显然，只要把这个速度取相反数就可以还原出原 flag 图案了（显然碰撞是可逆的）。

然而我并不想对着 bytecode 翻译一遍代码，所以我决定动态“注入”到 2.pyc 里面改变量。下面我们先把 2.pyc 重命名成 w2.pyc，因为不能直接 import 2。

但是 import w2 后，import 没返回，窗口已经运行了，有点难改变量。下面开始乱搞！

我们可以新建一个 pygamx.py 来 mock pygame，然后修改 2.pyc 的 bytecode：暴力把 pygame 改成 pygamx（暴力替换二进制数据即可）。

pygamx.py：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import pygame

class Time:
    class Clock:
        def init(self):
            self.first = True
            self.clock = pygame.time.Clock()

        def tick(self, fps):
            # 手动控制每一帧
            input()
            # self.clock.tick(fps)

            if self.first:
                self.first = False

                # 经过测试，可以在这里反向 import 并访问 Pointlist 而不抛出 AttributeError
                import w2
                for i in range(len(w2.Pointlist)):
                    p = w2.Pointlist[i]
                    w2.Pointlist[i] = w2.Point((p.x, p.y), -p.vx, -p.vy)

time = Time()

# mock 其它 attribute
init = pygame.init
quit = pygame.quit
mixer = pygame.mixer
display = pygame.display
event = pygame.event
draw = pygame.draw
QUIT = pygame.QUIT

然后经过测试，可以在上面 pygame.time.Clock.tick 里面反向 import w2，修改 list_ 和 Pointlist，把速度取反，就可以了。

此时直接运行 python w2.pyc，并且在控制台窗口用回车控制每一帧，看到 flag 差不多展示出来了就行了：

阵列恢复大师

数据恢复软件都是浮云，手撕才是正道。

当时做题的时候，看着 RAID 5 通过的人比 RAID 0 多，所以就先跑去做 RAID 5 了。后来仔细思索一下，可能是因为 RAID 5 有软件能一键恢复吧。

1 - RAID 0

额，在恢复之前，先来看一下 RAID 0 的结构。

说白了大概就是按块大小分块，然后按顺序依次存放在各个盘中。所以一个推论就是，一段内容只会出现在一个盘里面。

为了方便起见，先把硬盘名字按照字母序重命名成 1~8.img。

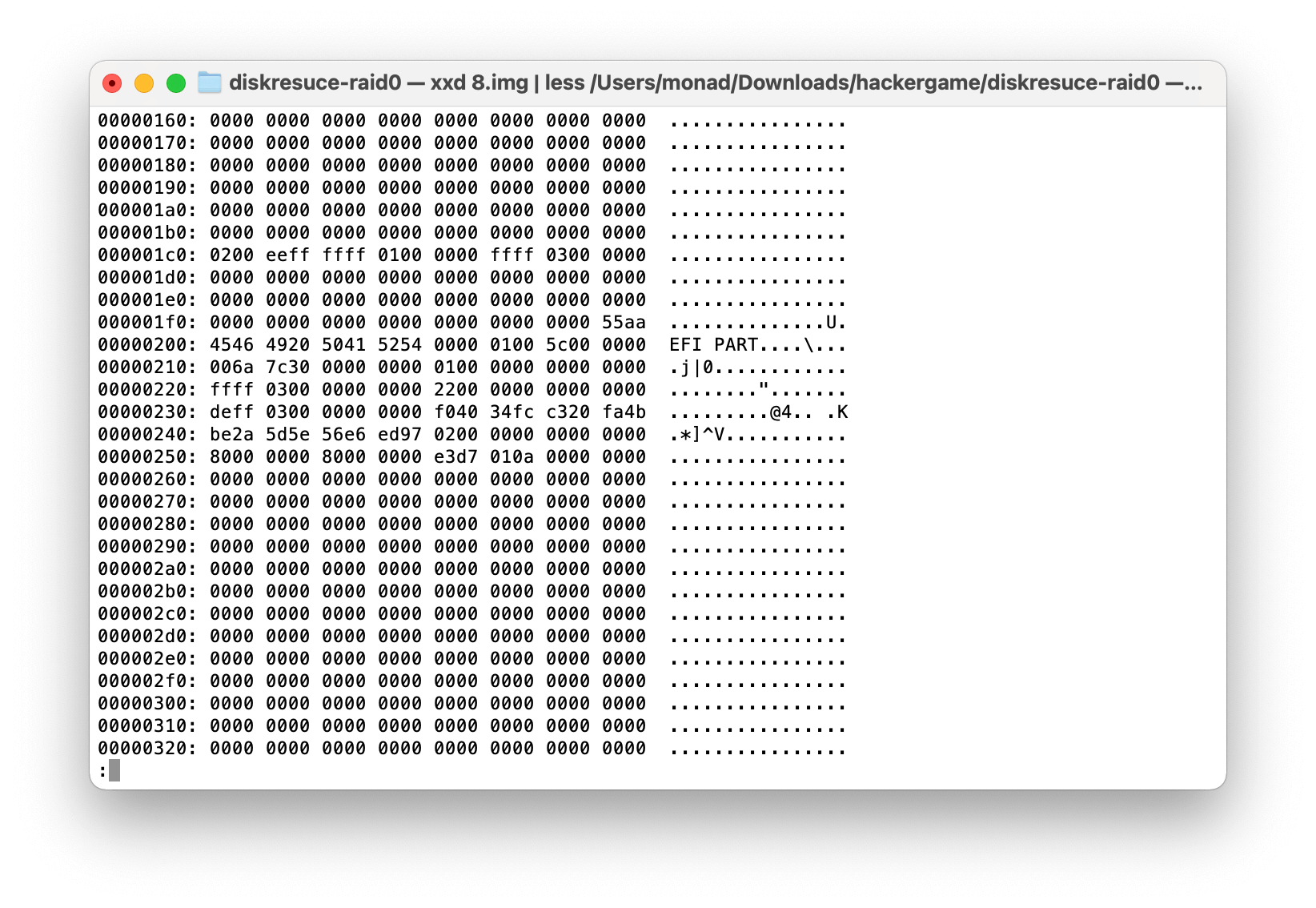
先随便看看这些盘的内容，然后不难发现，8.img 的 0x00000200 处有一个 EFI PART，这是 GPT 分区表的标志。于是就不难推测出 8.img 是第一个盘。

然后的话，再随便翻翻这些盘的内容，发现似乎空的部分（0x00）比较多。要确定盘的顺序的话，因为块与块之间是直接拼起来的，所以可以直接看内容的连续性来判断块的顺序，进而判断盘的顺序。

这样的话，随便翻看几下，发现 0x008C0000 和 0x008E0000 附近的内容有断层，而且丰富性比较高，有文本、乱码、零。并且从这两个“断层”的距离不难推测出块的大小是 128KB。（注意下面第 4 块盘的 0x008E0000 前的部分，n 后面应该有一个空格。）

Disk 0x008C0000 前 0x008C0000 后 0x008E0000 前 0x008E0000 后
1 0x00000000 2J..`...HD.....k Subtype /Link /R 0x00000000
2 0x00000000 ect [118.3625 23 g_system_respons 0x00000000
3 0x00000000 iveness_under_lo ...:......b.<.dL 0x00000000
4 0x00000000 .q,.[.Q..B....Y. 0470796 00000 n 0x00000000
5 0 obj.<< /A 489 ..g..b.c.D\...G. F.O...\i...o.G.. 0x00000000
6 0x00000000 000 n .000007636 M.t.p...V+.,=.2. 0x00000000
7 0x00000000 .0000470505 0000 4....%......,.iI 0x00000000
8 0x00000000 0 R /Border [ 0 n .0000076610 00 .0..TL$w.......1

根据 RAID 0 的结构，不难推测出 1 - 2，2 - 3，4 - 7，5 - 8，8 - 6（能分成三大块：5 8 6，1 2 3，4 7）。（如果觉得看表难推测的话，可以再看看这些位置的上下文，找一下文本的规律（常见词等）。）

到这里，可能的盘的顺序就只剩下 8 6 1 2 3 4 7 5 和 8 6 4 7 1 2 3 5 两种，已经很优了。如果懒的话，可以直接两种方法都试一下，看看哪种对的就行了。

实际上，在 0x001C0000 ~ 0x001E0000 的地方，可以观测到内容从有（非 0x00）变无（0x00）：

Disk 1 2 3 4 5 6 7 8
Not 0x00? T partial F F F T F T

据此，能推断出第 2 块盘在第 4 个位置。也就是说上面的两个方案，8 6 1 2 3 4 7 5 是对的。

既然顺序和块大小（128 KB）都有了，直接恢复出完整镜像（我用了一下 DiskGenius），然后把镜像挂载一下就行了。

2 - RAID 5

同理，先来看看 RAID 5 的结构。

与上面 RAID 0 不同的是，它多了一块奇偶校验块。

也像上面一样，先瞅瞅这些盘的头部。

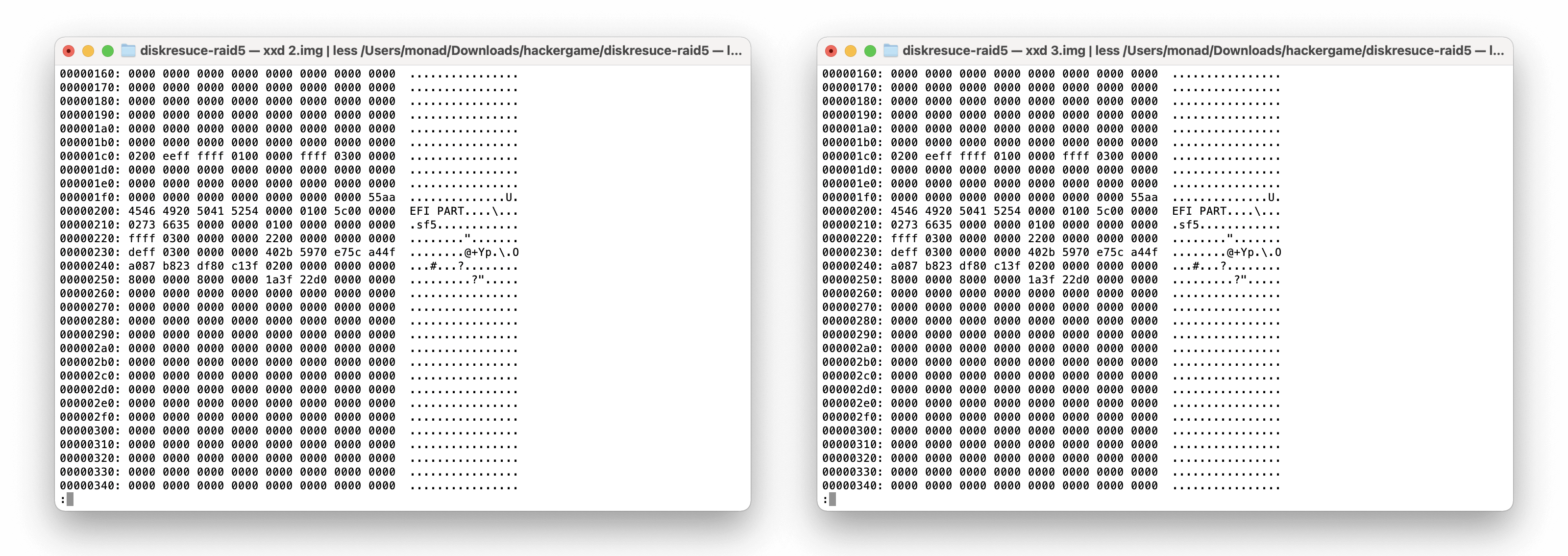
然后可以发现 2.img 和 3.img 有 GPT 头，故可以确定这两个盘一个是第一个位置，另一个是最后一个位置（首个校验块所在盘）。而且在 2.img 的 0x0040400 的地方可以找到 ext2/3/4 的 superblock。

所以现在就只剩下 12 种方案了……这一次我比较懒，就没有继续了（而且也懒得分析比较复杂的 RAID 5 了）。

然后我真的就去莽了，块大小 64 KB 和 256 KB 都莽一下（不要问我为什么不试 128 KB），再把上面 12 种方案都过一遍。实际操作就是在 DiskGenius 上排顺序，看看那个拼好了之后，DiskGenuis 能找到 ext2/3/4 分区。

最后试了几下，试出来了 2 4 1 5 3（块大小忘了实际上是多少了），然后用 DiskGenius 导出镜像（不知道为啥我那玩意不支持导出大于 1 MB 的文件），然后瞎搞一下，mount 上了就行了。

为什么我导出镜像之后还要用 testdisk 找一下分区后，导出分区才能挂载。

助记词

说句实话，这道题一点也不 math。

第一顿大餐

下载程序源码，打开。

其中 cn.edu.ustc.lug.hack.mnemonic_phrase.Instance 里的 post 是主要逻辑（flag 的处理也在这里），并且不难发现，这个函数里面有一个 for 循环，调试一下，发现每次请求好像只会循环一次。

回头看 HTTP API，发现似乎可以一次性提交一个数组，尝试一下提交 32 个相同的助记词，然后发现正好可以拿到第一个 flag。

第二顿大餐

作为一个逆向过 Minecraft 种子生成的人，怎么会止步于此呢

观察发现，sleep 函数是在 Phrase.equals 方法中执行的，然后我们并没有在本项目中发现直接调用它的地方。

再思考一下，能发现它会在 Set<Phrase>（实际上是 LinkedHashSet）中被 Set 调用。

第二个 flag 需要卡顿 9 秒，掐指一算，大概需要调用 equals 450 次，大概是 n2n^2n2 的级别。

查看 LinkedHashSet 源代码，猜测一下，我们要构造 hash 相同的 Phrase，让 Set 进行 n2n^2n2 级别次数的比较。

然后看 Phrase.hash 方法：

1
2
3
4
@Override
public int hashCode() {
    return Objects.hash(this.text, this.time, this.user);
}

再看 Object.hash 方法：

1
2
3
public static int hash(Object... values) {
    return Arrays.hashCode(values);
}

再看 Arrays.hashCode 方法：

1
2
3
4
5
6
7
public static int hashCode(Object a[]) {
    if (a == null) return 0;  // 在这个例子中与这个无关
    int result = 1;
    for (Object element : a)
        result = 31 * result + (element == null ? 0 : element.hashCode());
    return result;
}

换句话说，就是分别对 this.text, this.time, this.user 分别调用 .hashCode()，然后再拼在一起。这里先看 this.text（即 String）的 hashCode。

String.hashCode：

1
2
3
4
5
6
7
8
9
10
public int hashCode() {
    int h = hash;
    if (h == 0 && value.length > 0) {
        char val[] = value;
        for (int i = 0; i < value.length; i++)
            h = 31 * h + val[i];
        hash = h;
    }
    return h;
}

这个函数就是首先做了一个缓存，如果 hash（String 的一个 field）存在，就不算了。主要逻辑在 for 循环上。

我们可以把这个算法提取出来，暴力算 6004600^46004 种 hash（其实也可以双向 BFS，我这里没用）。

下面的暴力代码用 Rust 写，并且进行了一点小优化（因为算 hashCode 的过程是线性的），大概 5 分钟能跑完全部 6004600^46004 种 hash：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
use std::collections::HashMap;
use std::num::Wrapping;

const MNEMONICS_TEXTS: [&str; 600] = [ ... ];
const POW_31: [u32; 15] = [ 1, 31, 961, 29791, 923521, 28629151, 887503681, 1742810335, 2487512833, 4098453791, 2498015937, 129082719, 4001564289, 3789408671, 1507551809 ];
// POW_31[i] 记录的是 pow(31, i) 的结果

struct Mnemonics {
    pow: u32,
    hash: u32,
}

fn hash_str(s: &str) -> u32 {
    let mut x = Wrapping(0);
    for c in s.chars() {
        x = x * Wrapping(31) + Wrapping(c as u32);
    }
    x.0
}

impl Mnemonics {
    pub fn new(_index: usize, text: &'static str) -> Mnemonics {
        Mnemonics {
            pow: POW_31[ text.len() ],
            hash: hash_str(text),
        }
    }
}

fn join_hash(ss: &[&Mnemonics]) -> u32 {
    let mut x = Wrapping(0);
    let mut first = true;
    for s in ss {
        if !first {
            x = x * Wrapping(31) + Wrapping(' ' as u32);
        }

        x = x * Wrapping(s.pow) + Wrapping(s.hash);

        first = false;
    }

    x.0
}

fn main() {
    let mut mnemonics = Vec::new();
    for (i, text) in MNEMONICS_TEXTS.iter().enumerate() {
        mnemonics.push(Mnemonics::new(i, text));
    }

    // 我们只收集 hashCode 为 [0, 20) 的
    // 这样取是没问题的，假设 hash 足够均匀的话
    const HASH_RANGE: u32 = 20;
    let mut result = HashMap::new();

    for hash in 0..HASH_RANGE {
        result.insert(hash, Vec::new());
    }

    for (i1, m1) in mnemonics.iter().enumerate() {
        for (i2, m2) in mnemonics.iter().enumerate() {
            for (i3, m3) in mnemonics.iter().enumerate() {
                for (i4, m4) in mnemonics.iter().enumerate() {
                    // 这个 \times 31 下面会提到
                    let hash = join_hash(&[&m1, &m2, &m3, &m4]).wrapping_mul(31);
                    if hash >= HASH_RANGE {
                        continue;
                    }

                    let plan = [i1, i2, i3, i4];
                    result.get_mut(&hash).unwrap().push(plan);
                }
            }
        }
    }

    println!("{:?}", result);
}

上面的程序只会输出 hashCode 对应的单词的序号。

再写个程序解析这个输出（把两个程序分开，进行下面的操作的时候就不用重复破解 hash）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
s = [ ... ]  # 单词表
p = { ... }  # 上面的输出
d = [ ... ]  # delay，见下面的文字

results = []

i = 0
while i < 32:
    for x in p[20 - d[i]]:
        results.append('"{}"'.format( ' '.join([ s[i] for i in x ] )))
        i += 1
        if i >= 32 or d[i - 1] != d[i]:
            break

t = ', '.join(results)
print(f'[{t}]')

但是直接把暴力出的结果扔进程序里，发现最多只能卡 3 秒左右，是怎么回事？

我们继续看回去那个加单词的循环，把每一次循环所需的时间输出，就可以发现它的时间是 24 - 49 - 71 - 103 - ... - 254 - 0 - 24 - 47 - ... - 243 - 0 - 23 - ...（数字不是复制的，但是趋势是一样的）。

Phrase.hash 是 Objects.hash(this.text, this.time, this.user);，每过一秒，this.time 的变化就会使我们精心构造的 hash 冲突给毁掉。

这个有点难处理，观察回 Arrays.hashCode，我们可以把 this.text.hashCode * 31 后的 hash 缓存起来，每次当 this.time 加一的时候，我们就让 this.text.hashCode * 31 减一。

至于在这个长度为 32 的序列中，应该什么时候减一的这个问题，我也没有好的思路，只是随便试，试了一个相对较好的：

1
d = [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9 ]

由于实际运行时的微妙时间差（即开始运行的时候，并不是完全正对着每秒的开头的），所以要在在线的网站上多试几次。

马赛克

这道题的简单题意就是，给你一个打了码的二维码，并且给出打码的程序（算法是模糊部分的一个大的 block 的颜色，是这个区域内颜色的平均值）。简单算一下信息量，感觉还是能复原的。

一些用词（为了避免混乱所以先说明）：二维码的块：指模糊前的二维码的一个黑白块；码的块：指打码部分的一个色块（应该没毛病吧）。

于是乎，最朴素的方法就是……枚举原二维码每个块的黑白，然后看看跟模糊后的是否一致，但是这样做时间成本太大了。

然后可以发现，这个码的一个块的影响范围是有限的，大概就 10 个左右的二维码块。于是我们就可以针对每个码的块，枚举其下的二维码的黑白。再把每一个块的有效方案拼起来即可。

原理听懂了吗？原理大概就这个样子。但是……你发现这个确实并不好实现（大概?）

具体实现的话，假设前面处理了若干个块，这些块拼在一起的有效方案（可能有多个）放在一个数组 p 里。然后处理一个新的块的时候，就把当前区域的方案，与 p 中的匹配（能相容的就结合），把新的方案放到一个新的数组 q 供下一轮使用。

具体代码（调试输出十分炫酷，建议运行）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
import random
import math
import numpy as np
from PIL import Image

X, Y = 103, 137     # 马赛克左上角位置(单位为像素)
N = 20              # 马赛克块的数量（共N*N块）
BOX_SIZE = 23       # 每个马赛克块的大小（边长，单位为像素）
PIXEL_SIZE = 11     # 二维码每个块的大小（边长，单位为像素）


def calc_block_color(img, x, y):
    x1 = X + x * BOX_SIZE
    x2 = X + (x + 1) * BOX_SIZE
    y1 = Y + y * BOX_SIZE
    y2 = Y + (y + 1) * BOX_SIZE
    return math.floor(img[x1:x2, y1:y2].mean())


def check_qr_block_in(mx, my, qx, qy):
    # 检查 (qx, qy) 这个二维码块 是否影响 (mx, my) 这个打码块
    X1 = X + mx * BOX_SIZE
    X2 = X + (mx + 1) * BOX_SIZE - 1
    Y1 = Y + my * BOX_SIZE
    Y2 = Y + (my + 1) * BOX_SIZE - 1

    x1 = qx * PIXEL_SIZE
    x2 = (qx + 1) * PIXEL_SIZE - 1
    y1 = qy * PIXEL_SIZE
    y2 = (qy + 1) * PIXEL_SIZE - 1

    if (X1 <= x1 <= X2 and Y1 <= y1 <= Y2) or (X1 <= x1 <= X2 and Y1 <= y2 <= Y2) \
    or (X1 <= x2 <= X2 and Y1 <= y1 <= Y2) or (X1 <= x2 <= X2 and Y1 <= y2 <= Y2):
        return True
    return False


def paint_with(img, x, y, color):
    # 将 (x, y) 二维码块涂成 color 色
    x1 = x * PIXEL_SIZE
    x2 = (x + 1) * PIXEL_SIZE
    y1 = y * PIXEL_SIZE
    y2 = (y + 1) * PIXEL_SIZE
    img[x1:x2, y1:y2] = color


class Plan:
    def __init__(self, plan = None):
        if plan is None:
            plan = {}
        self.plan = plan
        self.min_x = 10000
        self.min_y = 10000

    def compatible(self, other):
        # 检查此 plan 是否与 `other` 兼容
        for (x, y), value in self.plan.items():
            if (data := other.plan.get((x, y))) is not None and data != value:
                return False
        return True

    def push(self, x, y, data):
        self.min_x = min(self.min_x, x)
        self.min_y = min(self.min_y, y)
        self.plan[(x, y)] = data

    def combine(self, other):
        # 将此 plan 与 `other` 结合，返回新的 plan
        assert self.compatible(other)
        new = Plan(self.plan.copy())
        for (x, y), value in other.plan.items():
            new.push(x, y, value)
        return new


def get_initial_plan(img):
    # 这是获取初始的 plan，主要包含码周边的一圈二维码块

    X1 = X + 0 * BOX_SIZE
    X2 = X + N * BOX_SIZE
    Y1 = Y + 0 * BOX_SIZE
    Y2 = Y + N * BOX_SIZE

    def is_in(x, y):
        return X1 <= x <= X2 and Y1 <= y <= Y2

    plan = Plan()

    for x, y in np.ndindex(57, 57):
        for i, j in np.ndindex(N, N):
            if check_qr_block_in(i, j, x, y):
                x1 = x * PIXEL_SIZE
                x2 = (x + 1) * PIXEL_SIZE - 1
                y1 = y * PIXEL_SIZE
                y2 = (y + 1) * PIXEL_SIZE - 1

                if not is_in(x1, y1):
                    color = img.getpixel((y1, x1))
                    plan.push(x, y, color)
                    break
                elif not is_in(x2, y2):
                    color = img.getpixel((y2, x2))
                    plan.push(x, y, color)
                    break

    POSITION_BLOCK = [(50, 50), (50, 28), (28, 50), (28, 28)]  # 定位块
    for block in POSITION_BLOCK:
        for x, y in np.ndindex(5, 5):
            d = max(abs(x - 2), abs(y - 2))
            color = 0 if (d % 2 == 0) else 255
            plan.push(block[0] + x - 2, block[1] + y - 2, color)

    return plan


def iter_blocks():
    # 枚举顺序从四周到中心，方便先利用已知数据
    for d in range(N):
        for i, j in np.ndindex(N, N):
            dx = min(i, (N - 1) - i)
            dy = min(j, (N - 1) - j)
            if min(dx, dy) == d:
                yield (j, i)


def main():
    mosaic = Image.open('pixelated_qrcode.bmp')
    temp = np.asarray(mosaic.copy(), dtype='uint8')

    plans = [ get_initial_plan(mosaic) ]
    for i, j in iter_blocks():
        new_plans = []

        related_block = []
        for x, y in np.ndindex(57, 57):
            if check_qr_block_in(i, j, x, y):
                related_block.append([x, y])
        n = len(related_block)

        print(f'Solving ({i:2}, {j:2}), related blocks: {n}')

        for b in range(2 ** n):
            plan = Plan()
            for index, block in enumerate(related_block):
                if ((2 ** index) & b) > 0:
                    paint_with(temp, *block, 0)
                    plan.push(*block, 0)
                else:
                    paint_with(temp, *block, 255)
                    plan.push(*block, 255)

            color = calc_block_color(temp, i, j)
            correct_color = mosaic.getpixel((Y + j * BOX_SIZE, X + i * BOX_SIZE))
            if color == correct_color:
                for old_plan in plans:
                    if plan.compatible(old_plan):
                        new_plans.append(old_plan.combine(plan))

        plans = new_plans

        if len(plans) > 1000:
            ids = [ i for i in range(len(plans)) ]
            random.shuffle(ids)
            buckets = []
            for i in ids[:1000]:
                buckets.append(plans[i])
            plans = buckets

        if len(plans) == 0:  # 如果 Failed 了，请洗把脸回来，再跑一遍
            raise Exception('Failed')

        # 比较炫酷的调试输出
        for x in range(9, 52):
            for y in range(12, 55):
                if (value := plans[0].plan.get((x, y))) is not None:
                    c = '*' if value == 0 else '_'
                else:
                    c = ' '
                print(c, end=' ')
            print()
        print(f'Current valid plans: {len(plans)}')

    # 输出 10 张复原的二维码
    for i, plan in enumerate(plans[:10]):
        for (x, y), value in plan.plan.items():
            paint_with(temp, x, y, value)
        image = Image.fromarray(temp, mode='L')
        image.save(f'result-{i}.bmp')


if __name__ == '__main__':
    main()

minecRaft

打开网页，我们发现了一个微型 Minecraft 游戏，然后就开始愉快的摸起鱼来。

咳咳，这是一道 web 题，并且「本题解法与原版 Minecraft 游戏无关」。故 F12 打开，然后可以看到 html 内嵌的 js 中有这么一段：

1
2
3
4
5
6
7
8
9
if (cinput.length >= 32) {
    let tbool = gyflagh(cinput.join(''));
    if (tbool) {
        pressplateList[65].TurnOn_redstone_lamp();
        content.innerText = 'Congratulations!!!';
        return;
    }
    cinput.length = 0;
}

并且 gyflagh 这个函数是定义在 flag.js 里面的，很难不猜测这就是最终涉及到 flag 的地方。

打开 flag.js，然后我们看到了一堆乱码…………

首先我们可以把 0x 打头的十六进制数转成十进制数，不然的话跟变量的命名很像，看着太瞎眼了。

然后观察一下参数是 422 到 439 之类的函数，可以发现都跟一个叫 _0x2c9e 的函数有关。

把这个 js 贴到 Devtools Console 里面，多执行几次，发现返回值不会变，并且都是 charCodeAt，slice, fromCharCode 这种函数名，不妨可以猜测这个函数只是一个 string mapping。所以我们就把这个 mapping 手动给它转回去。

替换完了之后，应该就只剩下变量名比较难看了。所以根据上下文，给这些变量换个名字。

这波操作下来之后，这个代码就好看了不少：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
String.prototype.encrypt = function(key_str) {
    const arr = new Array(2), key = new Array(4);
    let result = '';
    const plaintext = escape(this);
    for (var i = 0; i < 4; i++)
        key[i] = Str4ToLong(key_str.slice(i * 4, (i + 1) * 4));
    for (i = 0; i < plaintext.length; i += 8) {
        arr[0] = Str4ToLong(plaintext.slice(i    , i + 4));
        arr[1] = Str4ToLong(plaintext.slice(i + 4, i + 8));
        code(arr, key);
        result += LongToBase16(arr[0]) + LongToBase16(arr[1]);
    }
    return result;
};

function code(arr, key) {
    let a = arr[0], b = arr[1];
    const STEP = 2654435769, END = STEP * 32;
    let cur = 0;
    while (cur != END) {
        a += ((b << 4) ^ (b >>> 5)) + (b ^ cur) + key[cur & 3];
        cur += STEP;
        b += ((a << 4) ^ (a >>> 5)) + (a ^ cur) + key[(cur >>> 11) & 3];
    }
    arr[0] = a;
    arr[1] = b;
}

function Str4ToLong(val) {
    let result = 0;
    for (let i = 0; i < 4; i++)
        result |= val.charCodeAt(i) << (i * 8);
    return isNaN(result) ? 0 : result;
}

function LongToBase16(val) {
    let result = '';
    for (let i = 3; i >= 0; i--) {
        let tmp = ((val >> (8 * i)) & 0xff)['toString'](16);
        if (parseInt('0x' + tmp) <= 0xf)
            tmp = '0' + tmp;
        result += tmp;
    }
    return result;
}

function Base16ToLong(str) {
    let result = 0;
    for (let i = 0; i < 8; i += 2) {
        let tmp = parseInt('0x' + str.slice(i, i + 2));
        result = (result << 8) + tmp;
    }
    return result;
}

function LongToStr4(val) {
    return String.fromCharCode(val & 0xff, val >> 8 & 0xff, val >> 16 & 0xff, val >> 24 & 0xff);
}

function gyflagh(text) {
    let encrypted = text.encrypt('1356853149054377');
    return encrypted === '6fbde674819a59bfa12092565b4ca2a7a11dc670c678681daf4afb6704b82f0c';
}

我们先把目光放在 String.prototype.encrypt 上，这个函数首先将 key_str 分成了 4 段（1356 8531 4905 4377），然后将每一段通过 Str4ToLong 转为整数。

接着，再把 text（64 个字符，每 8 个分一段）分成 4 段，每一段中再分成前后两个部分（不妨称为 a, b），然后把 a, b 扔给 code 做变换，再把变换后的 a, b LongToBase16 后加到 result（字符串）后面。

上面这段话可能有点难理解，拿 gyflagh 中的例子来说，假设 text = "mInecRaft#-ls_900d_f0r_$ntEr1ain"，就是：

1
2
3
4
5
6
        Str4ToLong                   code                      LongToBase16

mIne cRaf  ->  1701726573 1717654115  -->   1874716276 -2120590913  ->  6fbde674 819a59bf
t#-l s_90  ->  1814897524 0809066355  -->  -1591700906  1531749031  ->  a1209256 5b4ca2a7
0d_f 0r_$  ->  1717527600 0610234928  -->  -1591884176  -965187555  ->  a11dc670 c678681d
ntEr 1ain  ->  1917154414 1852399921  -->  -1354040473    79179532  ->  af4afb67 04b82f0c

但是实际上，text 是什么我们是不知道的，我们要用 encrypted 来反推 text，其关键显然在 code 这个函数中。

然后现在的话，我们要完成的目标就是（右边的数值可以用 encrypted 进行 Base16ToLong 得到）：

1
2
3
4
code([?, ?], key)  ->   1874716276 -2120590913
code([?, ?], key)  ->  -1591700906  1531749031
code([?, ?], key)  ->  -1591884176  -965187555
code([?, ?], key)  ->  -1354040473    79179532

然后我们可以注意到，code 函数的计算是可逆的，可以通过最终的结果反推出输入的值。

于是随便写一个逆向程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const KEYS: [Wrapping<u32>; 4] = [ Wrapping(909456177), Wrapping(825439544), Wrapping(892352820), Wrapping(926364468) ];
const ADD: Wrapping<u32> = Wrapping(2654435769);

fn uncode(a: u32, b: u32) -> (u32, u32) {
    let mut val = ADD * Wrapping(32);

    let mut a = Wrapping(a);
    let mut b = Wrapping(b);

    for _i in 0..32 {
        b -= ((a << 4) ^ (a >> 5)) + a ^ val + KEYS[((val >> 11).0 & 3) as usize];
        val -= ADD;
        a -= ((b << 4) ^ (b >> 5)) + b ^ val + KEYS[(val.0 & 3) as usize];
    }

    return (a.0, b.0);
}

然后就不难推算出 code 的输入是：

1
2
3
4
[ 1700225869, 1598378594 ]
[ 1817013865, 1098007406 ]
[  861893681, 1601779041 ]
[ 1967743793, 1765372015 ]

然后再把这些值用 LongToStr4 拼回去，得到 McWebRE_inMlnCrA1t_3a5y_1cIuop9i。

密码生成器

运行密码生成器，发现并没有输入栏；并且能够感觉到，这道题是要“复现”输出。

然后，我们可以盲猜……这个程序的“输入”是，时间，精度大约是 1 秒。

然后的话，我们就可以把时间设置成 2021-09-22 23:11（也可以用 RunAsDate）（感觉那个时区只是一个障眼法），然后生成一些密码，多试几个，就成了。

密码是 $Z=CBDL7TjHu~mEX，登入就能获取 flag 了。

顺带一说，为了更方便手操（cao 一声），我还弄了一个自动读剪贴板的东西，这样鼠标就只用点“生成”、“复制到剪贴板”了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import win32clipboard
import time

s = set()
while True:
    while True:
        try:
            win32clipboard.OpenClipboard()
            break
        except Exception:  # 上面的 OpenClipboard 有概率出错，盲猜是读写冲突了
            pass

    data = win32clipboard.GetClipboardData()
    win32clipboard.CloseClipboard()

    if data not in s:
        print(f'new data: {data}')
        s.add(data)
    time.sleep(0.1)

JUST BE FUN

写在前面：这道题有更好的解法，甚至可以两维完成。我这里的话，首先是当时也没想那么多，基本上是“能跑就行”，其次我以为交换只能交换栈顶两个数，这个就限制了很多可能。所以这个解法看个乐就行。

说实话，这道题还是蛮有意思的。怎么说呢，看着自己写的指令在三维空间上执行，虽然实际上没有什么用，但是看起来炫酷就完事了。

这道题的大致意思就是，你可以在一个三维（256 * 256 * 256）的空间（可以看成是地址）上写程序（每个点能写一个指令），然后解析器会在上面跑。同时解析器会随机生成一个求值字符串，需要你编写一个能正确算出这个值的程序。

指令 机器码 读取数 写入数 含义
ADD_OP + 2 1 将栈顶两个数相加
SUB_OP - 2 1 将栈顶两个数相减（栈顶为减数）
MUL_OP * 2 1 将栈顶两个数相乘
DIV_OP / 2 1 将栈顶两个数相除（栈顶为除数）
MOD_OP % 2 1 将栈顶两个数取模（栈顶为模数）
NOT_OP ! 1 1 取非
CMP_OP ` 2 1 比较，栈顶小则 1，否则为 0
X_U_OP > 0 0 向 x+ 运行
X_D_OP < 0 0 向 x- 运行
Y_U_OP v 0 0 向 y+ 运行
Y_D_OP ^ 0 0 向 y- 运行
Z_U_OP [ 0 0 向 z+ 运行
Z_D_OP ] 0 0 向 z- 运行
X_JMP _ 1 0 若栈顶为 True，则向 x- 运行，反之亦然
Y_JMP | 1 0 若栈顶为 True，则向 y- 运行，反之亦然
Z_JMP # 1 0 若栈顶为 True，则向 z- 运行，反之亦然
STR_OP " 0 n 将此处（不含 "）到下一个 " 之前的指令，都作为 ASCII 写入栈中
DUP_OP : 1 2 将栈顶元素复制多一份
SWAP_OP \ 2 0 将两个指定位置的值交换（位置为相对于栈顶，不计这两个操作数，从 1 开始）
POP_OP $ 1 0 弹出栈顶一个元素
NUM_OP . 1 0 将栈顶作为数字写入 result
CHR_OP , 1 0 将栈顶作为 ASCII 写入 result
INP_OP ~ 0 1 读取 input 序列的下一个字符，为 ASCII 码
END_OP @ 程序结束
NOP_OP 0 0 什么都不做（按照惯性继续向前）

并且已知程序从 [0, 0, 0] 开始执行，方向为 [1, 0, 0]（x+）。

输入序列是像 6*2|2*4<2*6*1x7^4|3 一类的字符串，运算符没有优先级（都是从左向右），数字都是 1 位数字。运算符具体含义如下：

运算符 ASCII 含义
+ 43 加法
* 42 乘法
^ 94 幂运算
x 120 二进制异或（XOR）
| 124 二进制或（OR）
< 60 二进制左移

于是我们可以大致确定这个程序的框架：

  1. 先获取第一个数字，压入栈中，作为初始数值；
  2. 获取下一个输入（运算符），然后分发到不同的代码段中执行；
  3. 重复第 2 个操作，直到遇到 \0。

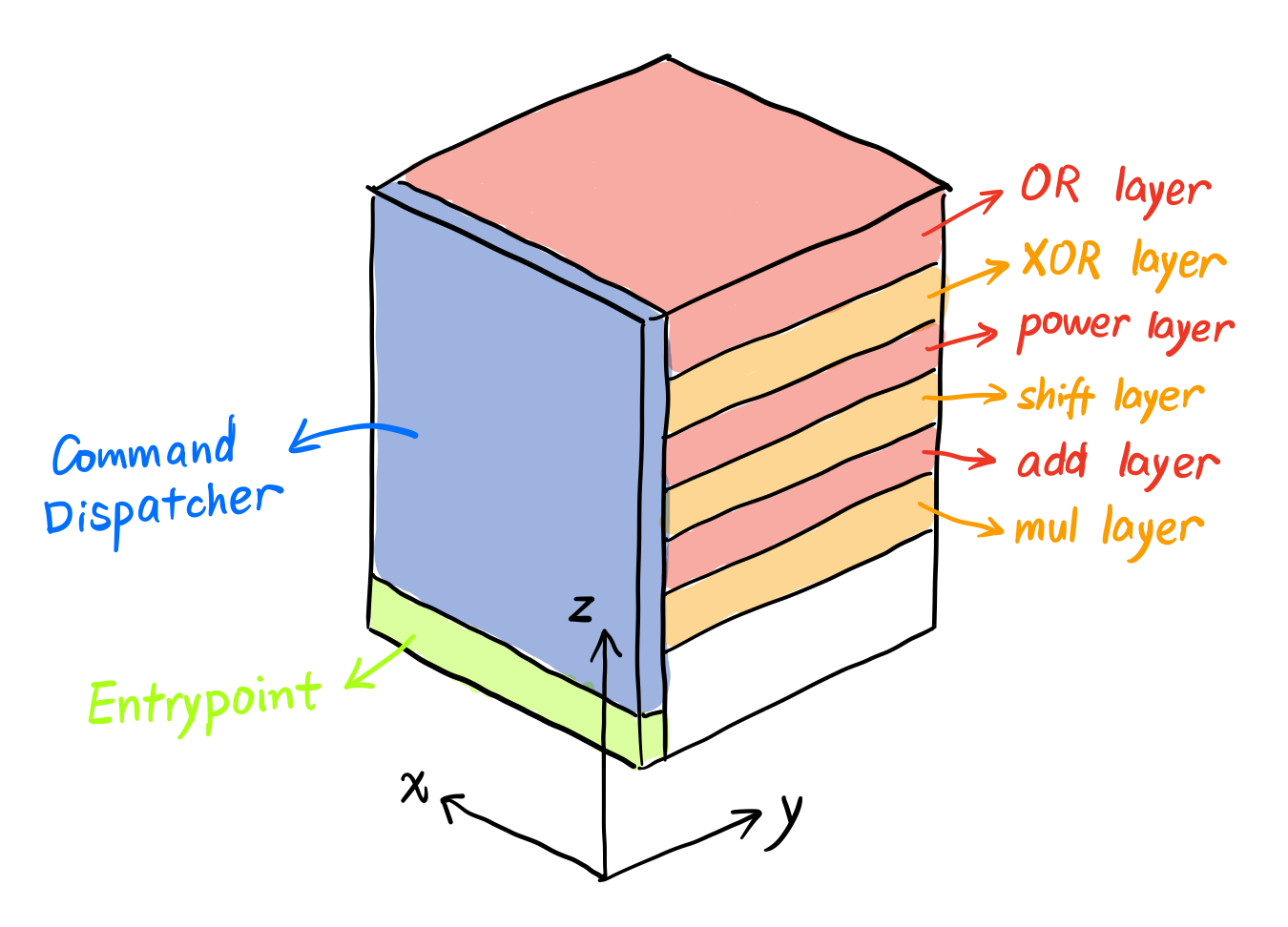
于是我们可以设计这么一种 layout：

注意到运算符的顺序，按照 ASCII 来排序可以方便后面的比较操作（只需要比较 > 一次就可以了，不用反过来再比一次）。

至于每一层，反正它给了 256 格高，我直接给每一层分配了 16 格的高度，让它们自由发挥，避免上下冲突。

下面我们来分别设计这些部分，目录：

Useful Patterns

在开始之前，我们先定义一些常用操作的 patterns。

比较栈顶位置与一个常数（0~9）

指令 栈 备注
[ val ]
DUP_OP [ val, val ] 栈顶元素需要保留，而比较指令会消耗参数，故复制一份
0~9 [ val, val, 0~9 ] 需要比较的常数
CMP_OP [ val, 0/1 ] 进行比较，并且把比较结果放到栈顶
... [ val ] 自定义跳转
POP_OP [] 如果整个匹配过程结束（val 不再需要）

比较栈顶位置与一个常数（超出 0~9）

如果范围超出了 0~9，就要考虑用字符串模式将比较常数压入栈中。

指令 栈 备注
[ val ]
DUP_OP [ val, val ] 栈顶元素需要保留，而比较指令会消耗参数，故复制一份
STR_OP [ val, val ] 进入字符串模式
x [ val, val, 'x' ] 需要比较的常数（比 9 大的数可以找 ASCII 后面的字母）
0 [ val, val, 'x', '0' ] 用来后面做减法
STR_OP [ val, val, 'x', '0' ] 退出字符串模式
SUB_OP [ val, val, x ] 减一下，获得真实数字
CMP_OP [ val, 0/1 ] 进行比较，并且把比较结果放到栈顶
... [ val ] 自定义跳转
POP_OP [] 如果整个匹配过程结束（val 不再需要）

比较栈顶位置与一个字符

跟上一个相比，不用压入 0 了。

指令 栈 备注
[ val ]
DUP_OP [ val, val ] 栈顶元素需要保留，而比较指令会消耗参数，故复制一份
STR_OP [ val, val ] 进入字符串模式
x [ val, val, 'x' ] 需要比较的字符
STR_OP [ val, val, 'x' ] 退出字符串模式
CMP_OP [ val, 0/1 ] 进行比较，并且把比较结果放到栈顶
... [ val ] 自定义跳转
POP_OP [] 如果整个匹配过程结束（val 不再需要）

交换栈顶两个元素

因为我一开始以为只能交换栈顶两个元素，等到实现到最后才发现不是。反正无伤大雅，加两个操作数就完事了。

指令 栈 备注
[ v1, v2 ]
1 [ v1, v2, 1 ]
2 [ v1, v2, 1, 2 ]
CMP_OP [ v2, v1 ] 观察 be_fun.py 代码，易得

Program Entrypoint

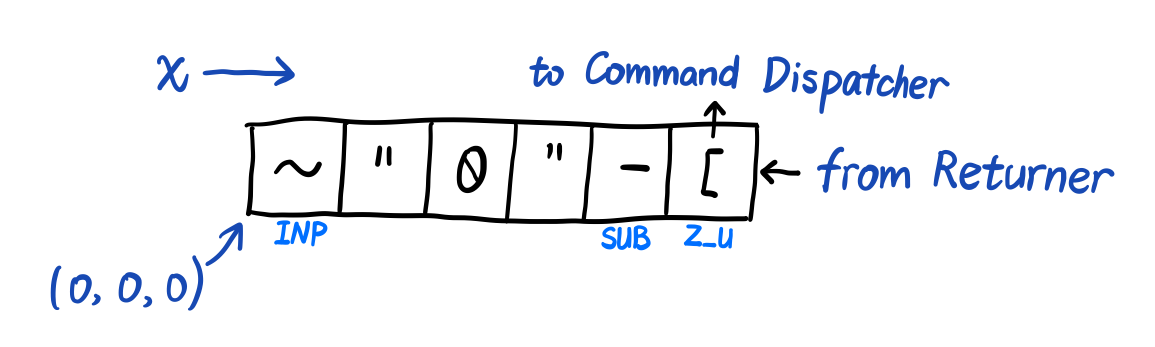
如图所示，获取第一个数字然后减去 0，然后向上跳转，将控制权交给 Dispatcher。

注意到这里还有一个 Returner，其实只是复用了一下这个 [ 字符，将 [ 看成两部分共用的即可。

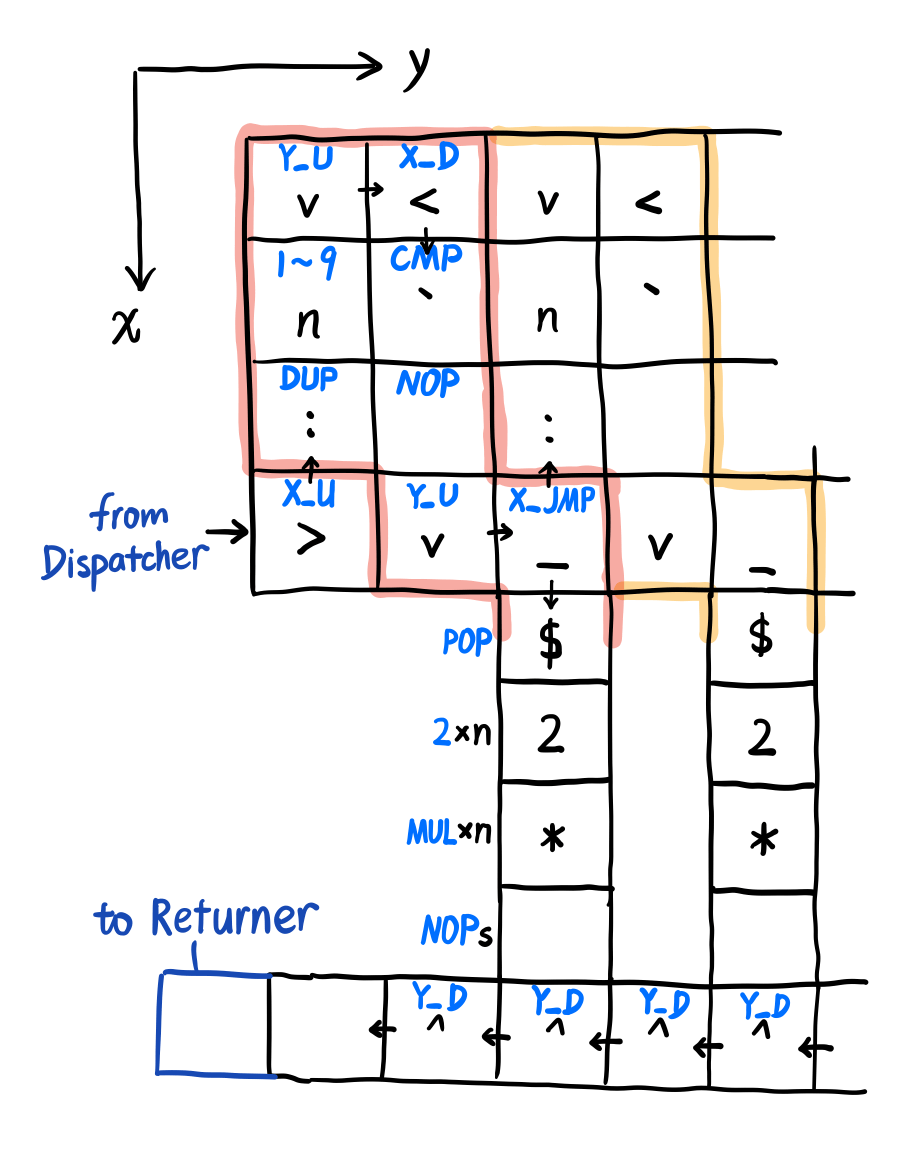
Command Dispatcher & Returner

这一 section 的指令全部都是放在 y=0 中。

左下角的地址，可以看作是新一轮运算执行的开始（后面 Returner 也会返回到这个位置）。

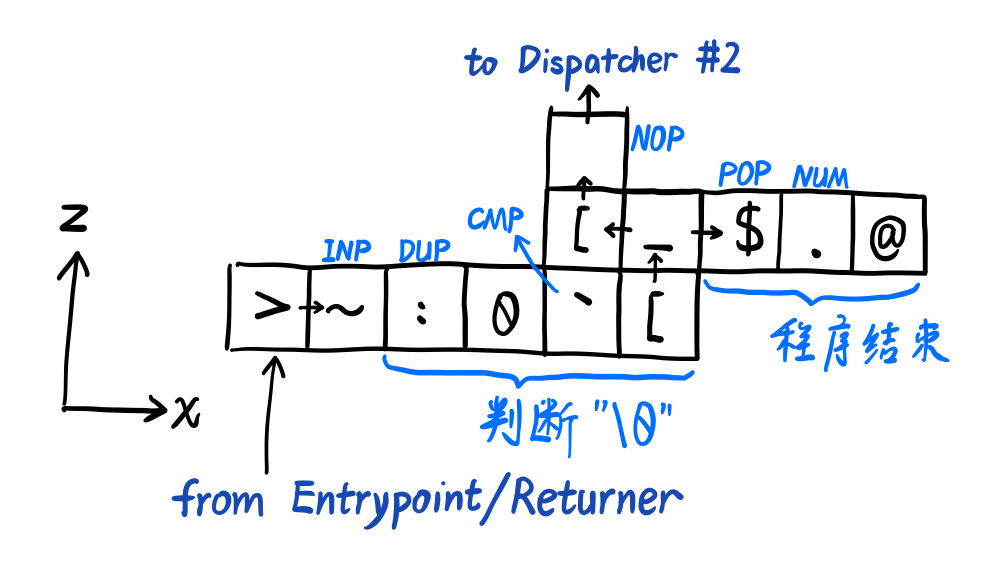
所以先获取这一轮的运算符，然后判断是不是 0，是 0 的话就写出结果，然后退出程序。

否则就向 z+ 运行，到对应 Command 的 layer 的时候，就比较一下运算符，比较成功就跳转进去（y+）。

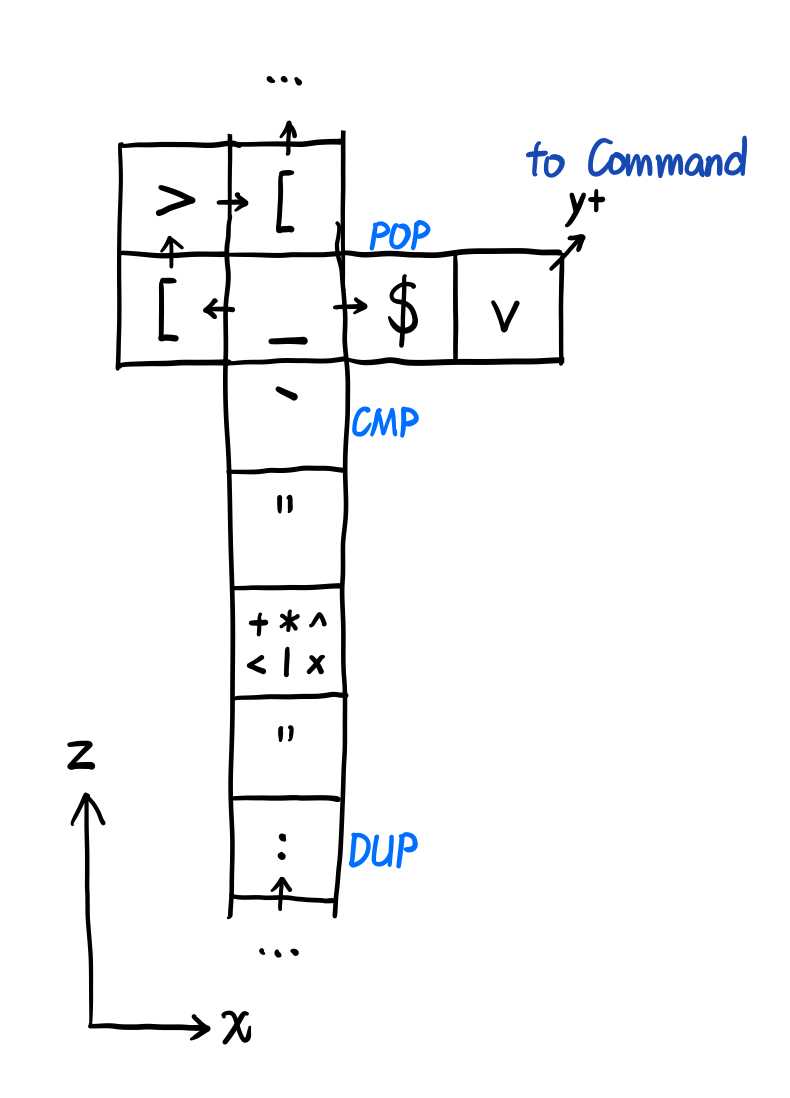
比较器如下所示，其中 +*^<|x 为这一层的 Command，根据情况安排：

至于 Returner 的话，我就直接在 x=245, y=0 的地方安排一条 Z_D_OP 的返回通道，指令运行完就跳到这个位置就行。

然后在 z=0, y=0 的地方，再安排一条返回 [5, 0, 0] 的 X_D_OP 通道（返回到 Entrypoint 的 from Returner 的地方，然后进入下一轮运算）

其实这个怎么搞也没有太大关系，先把标准弄好，后面对接的时候就会比较方便。

Binocular Operator

加法和乘法比较简单，甚至指令都是一维的，就不画图了。

指令 栈 备注
[ val ] 注意到运算符已经被提前 POP 出去了
INP_OP [ val, 'x' ] 获取运算数
STR_OP [ val, 'x' ] 进入字符串模式
0 [ val, 'x', '0' ]
STR_OP [ val, 'x', '0' ] 退出字符串模式
SUB_OP [ val, x ] 因为前面的 x 是字符，需要减一个 0
+ or * [ res ] 进行加法/乘法操作

这堆操作搞完了之后，就直接导航到 x=245, y=0 处就不用管了（控制权交给 Returner）。

Power and Shift Operator

这一段的操作主要是左移和幂。思考一下，虽然可以写一个简单循环，但是仔细想一下，发现细节还是挺多的，于是我就换了一个思路。

考虑到操作数只有 1 到 9 的范围，所以可以把这些把这些情况分开考虑（分别安排电路）。

对于左移操作，如果要左移 x 位的话，等价于乘上 x 个 2，于是我们就可以先压入 x 个 2，再执行 x 次乘法操作。

对于幂运算，就是把当前的 val 复制出 x 份，然后再执行 x - 1 次乘法即可。

上面划出来点部分可以往后堆叠，我本来想做成单片的，但是没做成。注意到这里的 n 是从小到大（即 1~9）排的。

对于幂操作也类似，在中间竖条的地方改成 DUP_OP 和 MUL_OP（都是 x - 1 次）即可。

Bitwise Operator

这个位运算，我一开始在想，怎么用加减乘除模这些运算凑出来一个位运算啊。然后想不出来（也可能是我太菜了）。

如果不能凑的话，考虑到操作数只有 1~9，最多就是二进制的低 4 位，也就是说，对于左操作数，只用考虑它的低 4 位就行了（0~15）。

然后掐指一算，9×16=1449 16 = 1449×16=144，感觉打个表完全可以接受啊，整个地址空间每维有 256 个长度，完全够用。

也就是说，我们首先要把左操作数的低 4 位提取出来，跟右操作数一起寻址（打表）（实际上为了方便起见，这两个部分分开寻址），然后找到结果之后再跟原数的高位结合，就可以了。

先把大框架搭起来，先把左操作数 val 拆成 16a+b16a + b16a+b 的形式（为了可读性，这里省略掉一些重复的部分）：

指令 栈 备注
[ val ]
DUP_OP [ val, val ] 复制一份，毕竟要拆成两个数
STR_OP [ val, val ] 进入字符串模式
'0' + 16 [ val, val, '@' ] 因为 16 超出了 0~9，只能这样干了
'0' [ val, val, '@', '0' ]
STR_OP [ val, val, '@', '0' ] 退出字符串模式
SUB_OP [ val, val, 16 ] 减一下，获得真正的 16
DIV_OP [ val, a ] 除一下，获得 a
1, 2, SWAP_OP [ a, val ] 交换栈顶俩元素
STR_OP [ a, val ]
* [ a, val, 16 ] 自行用 STR 压入 16（参考上面）
MOD_OP [ a, b ] 模一下，获得 b
... (P1) [ a ] 把 b 拿去匹配（寻址）
INP_OP [ a, 'x' ]
* [ a, x ] 自行减 0
... (P2) [ a ] 把 x 拿去匹配
STR_OP [ a ]
'0' + r [ a, 'r' ] 打表结果
'0' [ a, 'r', '0' ]
STR_OP [ a, 'r', '0' ]
SUB_OP [ a, r ]
... 这里可以先返回，后面的内容可以复用
1, 2, SWAP_OP [ r, a ]
* [ r, a, 16 ] 自行用 STR 压入 16（参考上面）
MUL_OP [ r, a * 16 ]
ADD_OP [ a * 16 + r ]

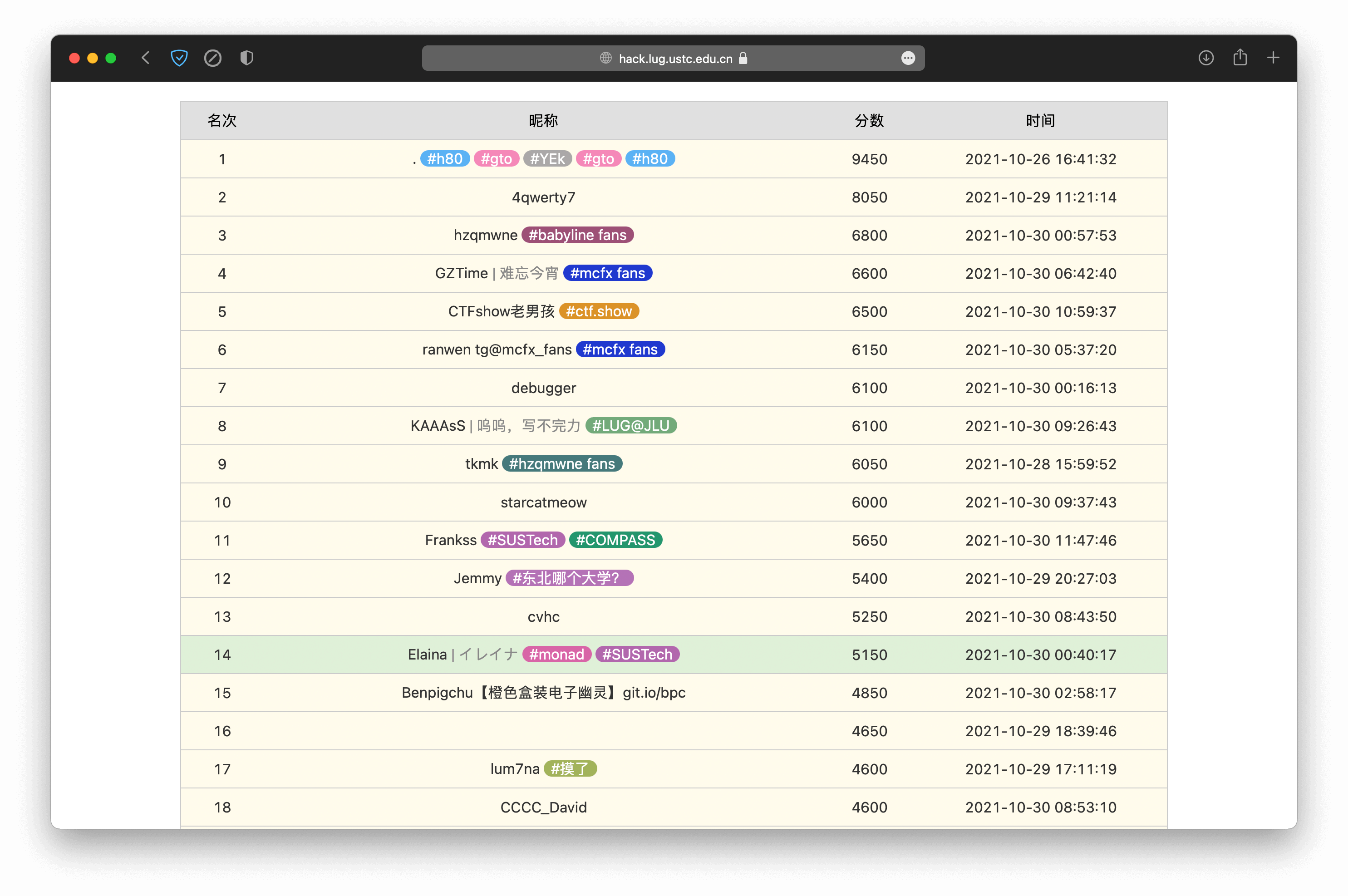
然后把子 dispatcher（P1、P2）写好就行了。由于打表，2 个变量就要用掉 2 维，还有一维要放匹配完后执行的指令，所以以下三维灵魂抽象画警告。

Layout
P1
P2

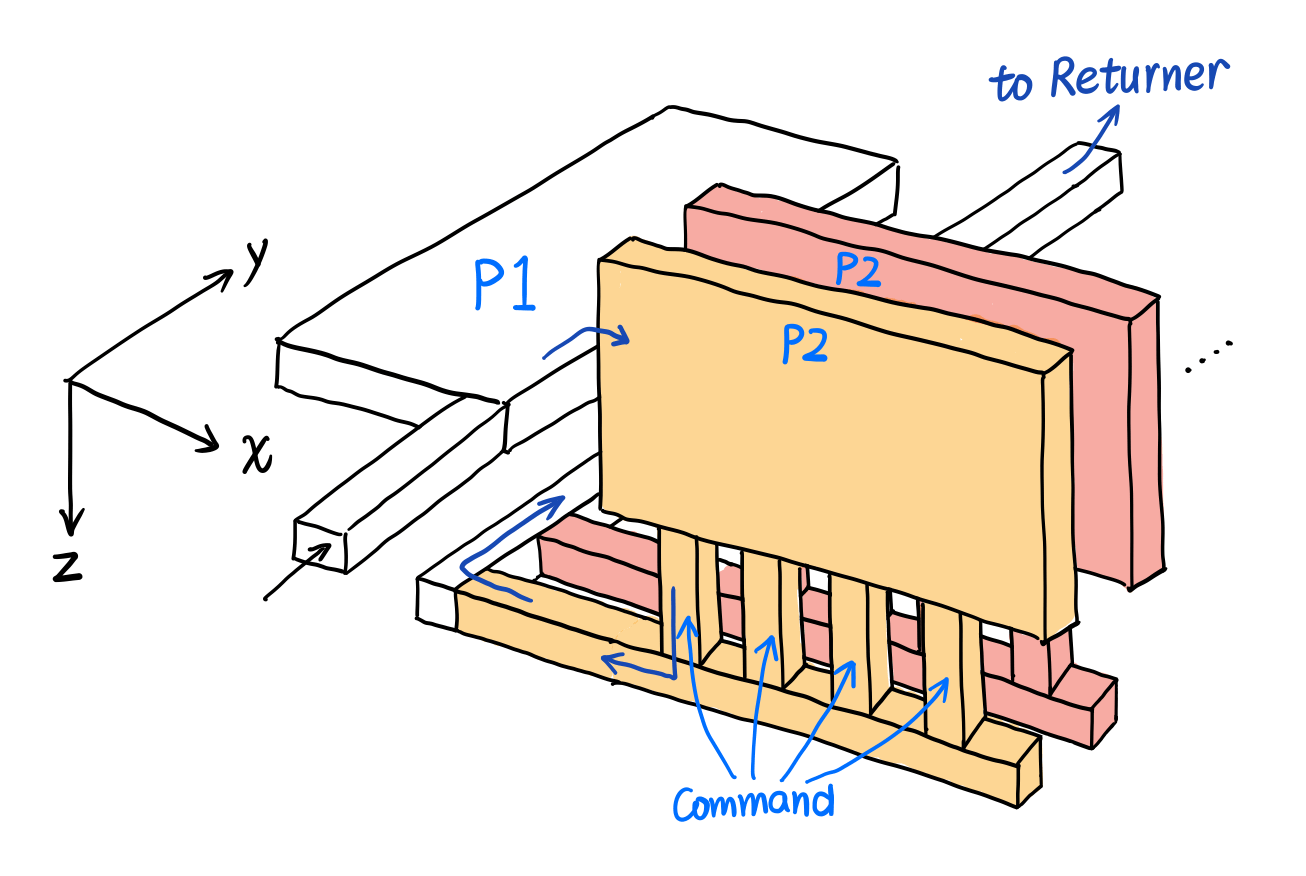
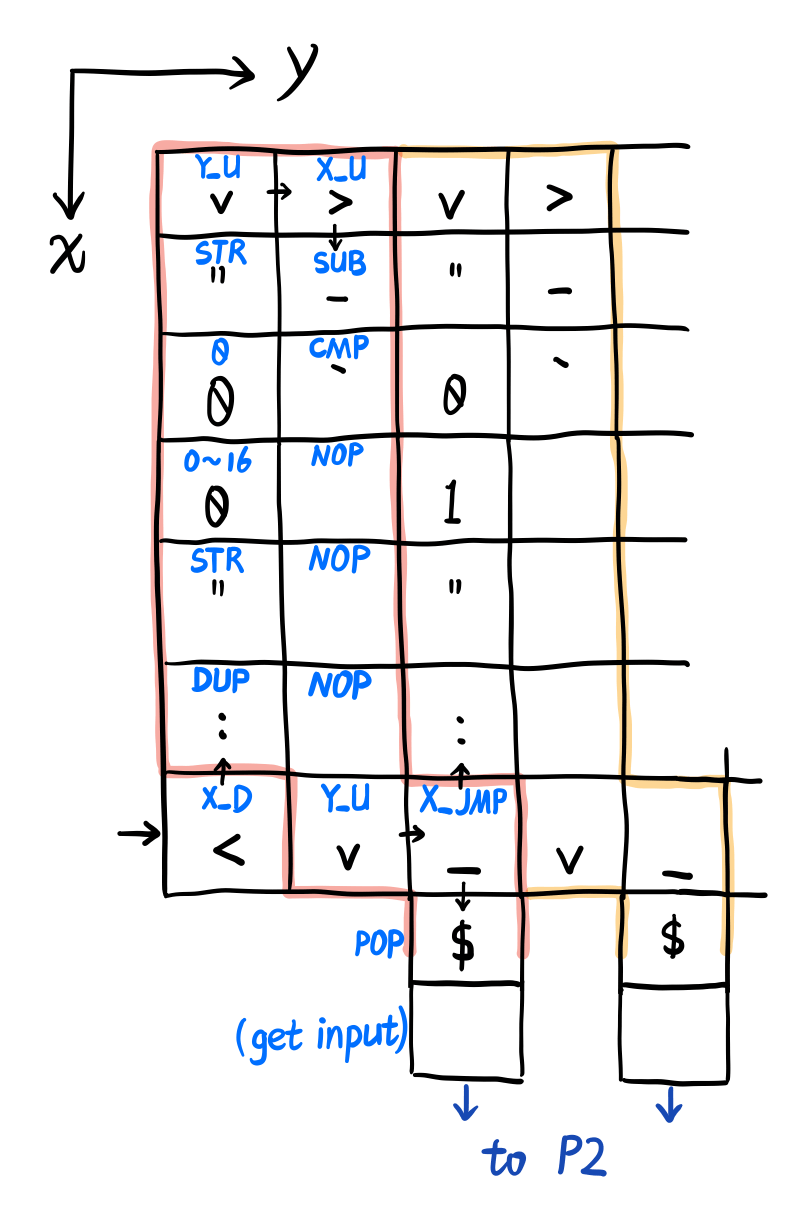
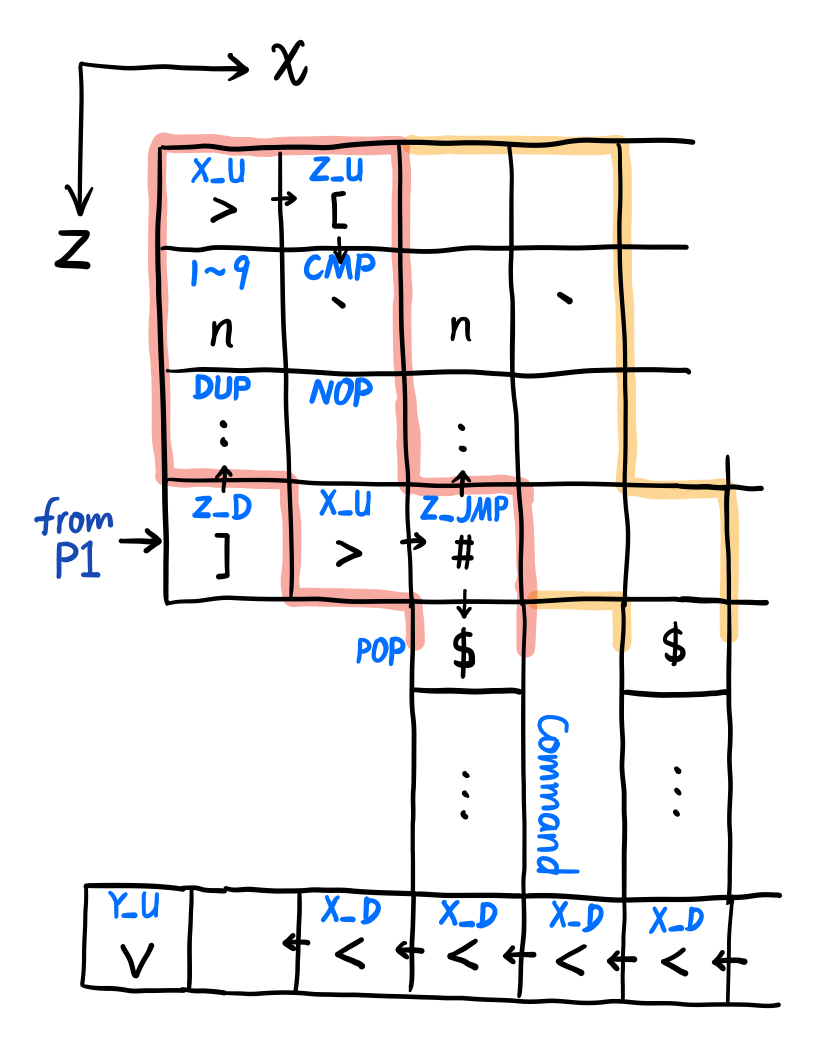
大概就是这个样子，相信大家都能看懂吧（）。

最后把所有的部分拼起来，就成了。代码呢，就是这个样子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
from pwn import *

TOKEN = '1:MEQCIBY0ubN3BOXYsuRdXzqWIWNf8Jx0Y6giZCSp/Rg8zdNwAiBMZGWaiIGLD33KTfQ5TTLejp9PwGp8Gg4HsJbdo8sVig=='

ADD_OP = '+'
SUB_OP = '-'
MUL_OP = '*'
DIV_OP = '/'
MOD_OP = '%'
CMP_OP = '`'
X_U_OP = '>'
X_D_OP = '<'
Y_D_OP = '^'
Y_U_OP = 'v'
Z_U_OP = '['
Z_D_OP = ']'
X_JMP = '_'
Z_JMP = '#'
STR_OP = '\"'
DUP_OP = ':'
SWAP_OP = '\\'
POP_OP = '$'
NUM_OP = '.'
INP_OP = '~'
END_OP = '@'
NOP_OP = ' '

def NUM(x):
    return chr(x + ord('0'))


board = [[['@' for i in range(0x100)] for j in range(0x100)] for k in range(0x100)]

BLOCK_START = 0x20
BLOCK_HEIGHT = 0x10

SUB_COMMAND = {
    '*': BLOCK_START + BLOCK_HEIGHT * 1, # 42
    '+': BLOCK_START + BLOCK_HEIGHT * 2, # 43
    '<': BLOCK_START + BLOCK_HEIGHT * 3, # 60
    '^': BLOCK_START + BLOCK_HEIGHT * 4, # 94
    'x': BLOCK_START + BLOCK_HEIGHT * 5, # 120
    '|': BLOCK_START + BLOCK_HEIGHT * 6, # 124
}


def load_init():
    for (i, c) in enumerate([INP_OP, STR_OP, '0', STR_OP, SUB_OP, Z_U_OP]):
        board[i][0][0] = c


def load_command_dispatcher():
    board[ 5][0][1] = X_U_OP
    board[ 6][0][1] = INP_OP
    board[ 7][0][1] = DUP_OP
    board[ 8][0][1] = NUM(0)
    board[ 9][0][1] = CMP_OP
    board[10][0][1] = Z_U_OP
    board[10][0][2] = X_JMP
    board[ 9][0][2] = Z_U_OP

    board[11][0][2] = POP_OP
    board[12][0][2] = NUM_OP
    board[13][0][2] = END_OP

    for z in range(3, 0x100):
        board[ 9][0][z] = NOP_OP

    for (cmd, pos) in SUB_COMMAND.items():
        for (i, c) in enumerate([DUP_OP, STR_OP, cmd, STR_OP, CMP_OP]):
            board[9][0][pos - (5 - i)] = c
        board[9][0][pos] = X_JMP
        board[10][0][pos] = POP_OP
        board[11][0][pos] = Y_U_OP
        board[8][0][pos] = Z_U_OP
        board[8][0][pos + 1] = X_U_OP
        board[9][0][pos + 1] = Z_U_OP


def load_returner():
    for x in range( 6, 0x100):
        board[x][0][0] = X_D_OP
    for z in range(1, 0x100):
        board[0x100 - 10][0][z] = Z_D_OP


def load_binocular_operator(cmd, op):
    Z_BASE = SUB_COMMAND[cmd]

    for (i, c) in enumerate([X_U_OP, INP_OP, STR_OP, NUM(0), STR_OP, SUB_OP, op]):
        board[11 + i][1][Z_BASE] = c

    for x in range(18, 0x100):
        board[x][1][Z_BASE] = NOP_OP
    board[0x100 - 10][1][Z_BASE] = Y_D_OP


def load_pow_operator():
    Z_BASE = SUB_COMMAND['^']

    for (i, c) in enumerate([NOP_OP, INP_OP, STR_OP, NUM(0), STR_OP, SUB_OP]):
        board[11][i + 1][Z_BASE] = c

    board[11][7][Z_BASE] = X_D_OP
    for i in range(1, 9 + 1):
        y = (i - 1) * 2 + 7
        board[10][y    ][Z_BASE] = DUP_OP
        board[ 9][y    ][Z_BASE] = NUM(i)
        board[ 8][y    ][Z_BASE] = Y_U_OP
        board[ 8][y + 1][Z_BASE] = X_U_OP
        board[ 9][y + 1][Z_BASE] = CMP_OP
        board[10][y + 1][Z_BASE] = NOP_OP
        board[11][y + 1][Z_BASE] = Y_U_OP
        board[11][y + 2][Z_BASE] = X_JMP
        board[12][y + 2][Z_BASE] = POP_OP

        x = 13
        for j in range(i - 1):
            board[x][y + 2][Z_BASE] = DUP_OP
            x += 1
        for j in range(i - 1):
            board[x][y + 2][Z_BASE] = MUL_OP
            x += 1
        while x < 0x100:
            board[x][y + 2][Z_BASE] = NOP_OP
            x += 1

    for y in range(1, 0x100):
        board[0x100 - 10][y][Z_BASE] = Y_D_OP


def load_shift_operator():
    Z_BASE = SUB_COMMAND['<']

    for (i, c) in enumerate([NOP_OP, INP_OP, STR_OP, NUM(0), STR_OP, SUB_OP]):
        board[11][i + 1][Z_BASE] = c

    board[11][7][Z_BASE] = X_D_OP
    for i in range(1, 9 + 1):
        y = (i - 1) * 2 + 7
        board[10][y    ][Z_BASE] = DUP_OP
        board[ 9][y    ][Z_BASE] = NUM(i)
        board[ 8][y    ][Z_BASE] = Y_U_OP
        board[ 8][y + 1][Z_BASE] = X_U_OP
        board[ 9][y + 1][Z_BASE] = CMP_OP
        board[10][y + 1][Z_BASE] = NOP_OP
        board[11][y + 1][Z_BASE] = Y_U_OP
        board[11][y + 2][Z_BASE] = X_JMP
        board[12][y + 2][Z_BASE] = POP_OP

        x = 13
        for j in range(i):
            board[x][y + 2][Z_BASE] = NUM(2)
            x += 1
        for j in range(i):
            board[x][y + 2][Z_BASE] = MUL_OP
            x += 1
        while x < 0x100:
            board[x][y + 2][Z_BASE] = NOP_OP
            x += 1

    for y in range(1, 0x100):
        board[0x100 - 10][y][Z_BASE] = Y_D_OP


def load_bitwise_operator(cmd, calc):
    Z_BASE = SUB_COMMAND[cmd]

    for (i, c) in enumerate([DUP_OP, STR_OP, NUM(16), NUM(0), STR_OP, SUB_OP, DIV_OP, NUM(1), NUM(2), SWAP_OP,
                             STR_OP, NUM(16), NUM(0), STR_OP, SUB_OP, MOD_OP]):
        board[11][i + 1][Z_BASE] = c

    board[11][17][Z_BASE] = X_D_OP
    for i in range(16):
        y = i * 2 + 17
        board[10][y][Z_BASE] = DUP_OP
        board[ 9][y][Z_BASE] = STR_OP
        board[ 8][y][Z_BASE] = NUM(i)
        board[ 7][y][Z_BASE] = NUM(0)
        board[ 6][y][Z_BASE] = STR_OP
        board[ 5][y][Z_BASE] = Y_U_OP
        board[ 5][y + 1][Z_BASE] = X_U_OP
        board[ 6][y + 1][Z_BASE] = SUB_OP
        board[ 7][y + 1][Z_BASE] = CMP_OP
        board[ 8][y + 1][Z_BASE] = NOP_OP
        board[ 9][y + 1][Z_BASE] = NOP_OP
        board[10][y + 1][Z_BASE] = NOP_OP
        board[11][y + 1][Z_BASE] = Y_U_OP
        board[11][y + 2][Z_BASE] = X_JMP

        for (i, c) in enumerate([POP_OP, INP_OP, STR_OP, NUM(0), STR_OP, SUB_OP]):
            board[12 + i][y + 2][Z_BASE] = c

        y_base = y + 2
        board[18][y_base][Z_BASE] = Z_D_OP
        for j in range(1, 9 + 1):
            x = (j - 1) * 2 + (18)
            board[x    ][y_base][Z_BASE - 1] = DUP_OP
            board[x    ][y_base][Z_BASE - 2] = NUM(j)
            board[x    ][y_base][Z_BASE - 3] = X_U_OP
            board[x + 1][y_base][Z_BASE - 3] = Z_U_OP
            board[x + 1][y_base][Z_BASE - 2] = CMP_OP
            board[x + 1][y_base][Z_BASE - 1] = NOP_OP
            board[x + 1][y_base][Z_BASE    ] = X_U_OP
            board[x + 2][y_base][Z_BASE    ] = Z_JMP

            for (i, c) in enumerate([POP_OP, STR_OP, NUM(calc(i, j)), NUM(0), STR_OP, SUB_OP]):
                board[x + 2][y_base][Z_BASE + 1 + i] = c

        for x in range(18, 0x100):
            board[x][y_base][Z_BASE + 7] = X_U_OP

    for y in range(1, 0x100):
        board[0x100 - 10][y][Z_BASE + 7] = Y_D_OP
    for (i, c) in enumerate([NUM(1), NUM(2), SWAP_OP, STR_OP, NUM(16), NUM(0), STR_OP, SUB_OP, MUL_OP, ADD_OP]):
        board[0x100 - 10][10 - i][Z_BASE + 7] = c


def get_board():
    board_list = []
    for x in range(0x100):
        for y in range(0x100):
            for z in range(0x100):
                if board[x][y][z] != END_OP:
                    b = ord(board[x][y][z])
                    board_list.append(f'({x}, {y}, {z}) -> {b}')

    board_list.append('END')
    return ' '.join(board_list)


def submit():
    c = remote('202.38.93.111', 10104)
    result = get_board()
    c.recv()
    c.sendline(TOKEN)
    c.recv()
    c.sendline(result)

    while True:
        print(c.recvline())


def main():
    load_init()
    load_command_dispatcher()
    load_returner()

    load_binocular_operator('+', ADD_OP)
    load_binocular_operator('*', MUL_OP)
    load_pow_operator()
    load_shift_operator()
    load_bitwise_operator('|', lambda x, y: x | y)
    load_bitwise_operator('x', lambda x, y: x ^ y)

    submit()


if __name__ == '__main__':
    main()

p😭q

这道题本质上就是如何用眼看音乐，是把频谱图转换为声波。

我本来以为这道题还要手撕 FFT 的，结果发现完全不用，首先给了代码，再者[见下文]，于是这道题就完全是一道工程题，只要会调库就可以了。

看源码，源码大致可以分成两个部分：正向 FFT，和 gif 生成。

我们就反过来“逆向”每一步就行了。

首先是读 gif，这个没啥好说的，只是细节比较多，直接上代码（趴）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
image = Image.open('flag.gif')

db_frames = []

for i, gif_frame in enumerate(ImageSequence.Iterator(image)):
    # 将 gif_frame 转为 [x, y, 3] 的三维数组
    frame = np.asarray(
            gif_frame.convert('RGB').getdata(),
            dtype=np.uint8
        ).reshape(gif_frame.size[1], gif_frame.size[0], 3)

    dbs = []  # 该 frame 中，频率对应的 dB

    for freq in range(0, num_freqs):
        for i, threshold in enumerate(list(range(min_db, max_db + 1, quantize))[::-1], start=1):
            x = threshold - min_db
            y = (freq * 2 + 1) * 2
            color = frame[x][y]
            if (color == white_pixel).all():
                dbs.append(i - 1)
                break

    db_frames.append(dbs)

随后就是要逆向这个 melspectrogram。看源代码：

1
2
3
4
5
6
7
8
9
spectrogram = (
    numpy.around(
        librosa.power_to_db(
            librosa.feature.melspectrogram(
                ...
            )
        ) / quantize
    ) * quantize
)

最外层，/ quantize, numpy.around, * quantize 就是将 dB 取整。

然后再里面一层，就是 librosa.power_to_db，看这个命名……盲猜一下……大概有个函数……可以把它反过来，还真有：librosa.db_to_power。

再里面一层，就是 FFT 大头，librosa.feature.melspectrogram，本来呢，我还做好准备要手撕 FFT 的，然后一查文档，发现好家伙，这函数也有逆函数 librosa.feature.inverse.mel_to_audio，这就省事了。

接下来的事就是把上面的过程反过来套一遍就可以了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
db_frames = [ ... ]  # 上面的 db_frames

frames = np.array(db_frames).transpose(1, 0)  # 交换两维，我也不知道为啥要这样，反正接口要对上就对了
frames += min_db
# 如果考虑上面的对 2 取整的话，实际上还要加上期望值 1 才对？

y = librosa.feature.inverse.mel_to_audio(
    librosa.db_to_power(frames),
    22050,  # sample_rate
    n_fft=fft_window_size,
    hop_length=frame_step_size,
    window=window_function_type
)

sf.write('origin.wav', y, 22050)

至此，我们就把 gif 逆向成了 origin.wav。

音频是「The flag is, F-L-A-G, 634,971,243,582」（数字是英语数字的读法）。